
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Приклади розв’язання задач з визначенням центра ваги
|
|
Приклад 7.1. Знайти координати центра ваги плоскої фігури, що зображена на рис. 7.29. Розміри наведено в см.
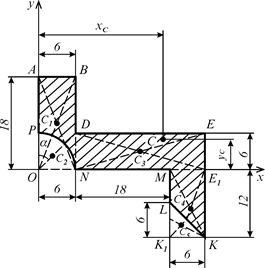
Рис. 7.29
Розв’язання. Для розв’язання використаємо метод розбиття в поєднанні з методом від’ємних площ. Виділимо в даній фігурі п’ять простих фігур (рис. 7.29):
7.1.1. Прямокутник OABN:
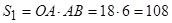 см2;
см2;
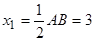 см;
см; 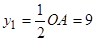 см.
см.
7.1.2. Круговий сектор ONP (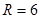 см,
см, 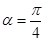 ):
):
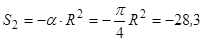 см2.
см2.
Беремо знак мінус, оскільки сектор є вирізаним.
Відрізок 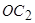 дорівнює
дорівнює
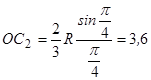 см.
см.
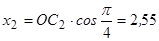 см;
см;
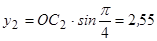 см.
см.
7.1.3. Прямокутник 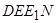 .
.
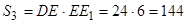 см2;
см2;
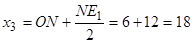 см;
см;
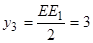 см.
см.
7.1.4. Прямокутник 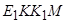 .
.
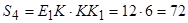 см2;
см2;
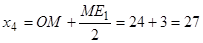 см;
см;
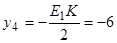 см.
см.
7.1.5. Трикутник 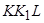 .
.
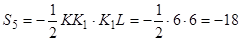 см2.
см2.
Беремо знак мінус, оскільки трикутник є вирізаний.
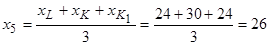 см;
см;
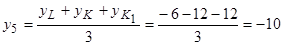 см.
см.
7.1.6. Координати центра ваги заданої плоскої фігури знаходимо за формулами (7.18)
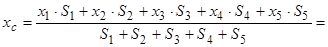
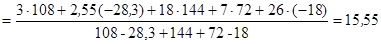 см;
см;

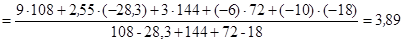 см.
см.
Відповідь: 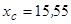 см;
см; 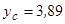 см.
см.
Приклад 7.2. На рис. 7.30 показано розріз тіла, який складається із циліндра, радіус якого 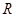 і висота
і висота 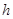 , і двох півкуль радіусами
, і двох півкуль радіусами 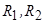 , центри яких співпадають з центрами нижньої і верхньої основ циліндра. Визначити центр ваги цього тіла, якщо
, центри яких співпадають з центрами нижньої і верхньої основ циліндра. Визначити центр ваги цього тіла, якщо
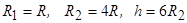 .
.
Розв’язання. Так як вісь 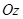 є для даного тіла віссю симетрії, то шуканий центр ваги С цього тіла лежить на осі
є для даного тіла віссю симетрії, то шуканий центр ваги С цього тіла лежить на осі 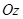 . Тому достатньо вирахувати тільки одну координату
. Тому достатньо вирахувати тільки одну координату 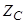 . Позначимо об’єми півкуль і циліндра відповідно
. Позначимо об’єми півкуль і циліндра відповідно 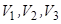 , а їх центри ваг
, а їх центри ваг 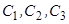 (рис. 7.30). Початок координат помістимо в точку
(рис. 7.30). Початок координат помістимо в точку 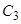 — центр ваги циліндра. Знайдемо об’єми і координати центрів ваг півкуль і циліндра.
— центр ваги циліндра. Знайдемо об’єми і координати центрів ваг півкуль і циліндра.
7.2.1. Перша півкуля.
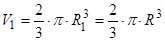 ;
;
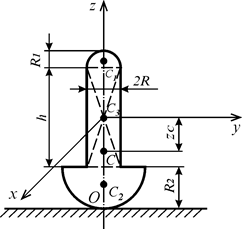
Рис. 7.30
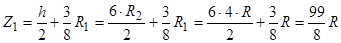 .
.
Примітка. Відстань від центра ваги півкулі радіусом 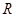 до її основи дорівнює
до її основи дорівнює 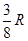 (див. рис. 7.15).
(див. рис. 7.15).
7.2.2. Друга півкуля.
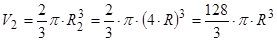 ;
;
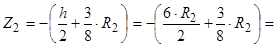
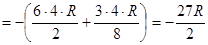 .
.
7.2.3. Циліндр.
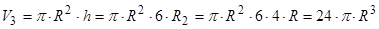
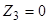 .
.
7.2.4. Шукану координату 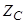 центра ваги даного тіла знаходимо по четвертій формулі із (7.16)
центра ваги даного тіла знаходимо по четвертій формулі із (7.16)
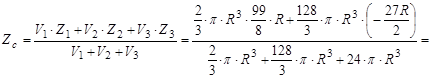
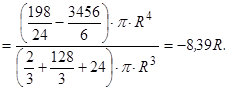
Відповідь: 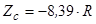 .
.
Приклад 7.3. Знайти координати центра ваги конструкції, яка складається із однорідних стрижнів (рис. 7.31), якщо ОА = 0, 6 м, АВ = 0, 6 м, ВН = 0, 3 м, ОD = 0, 9 м, DК = 0, 4 м.
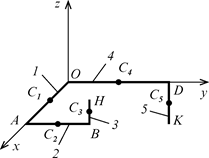
Рис. 7.31
Розв’язання. Для розв’язання використаємо метод розбиття конструкції на окремі частини ОА, АВ, ВН, ОD, DК, центри ваги яких визначаємо, використовуючи метод симетрії.
7.3.1. Координати центрів ваг цих частин такі:
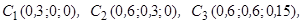
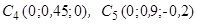 .
.
7.3.2. Довжини окремих частин конструкції дорівнюють:
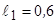 м;
м; 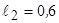 м;
м; 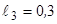 м;
м; 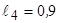 м;
м; 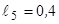 м.
м.
7.3.3. Центр ваги конструкції, складеної із однорідних стрижнів, знаходимо за формулами (7.14)
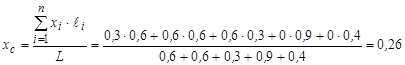 м;
м;
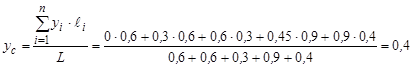 м;
м;
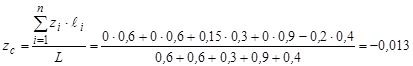 м.
м.
Відповідь: 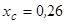 м;
м; 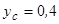 м;
м; 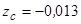 м.
м.
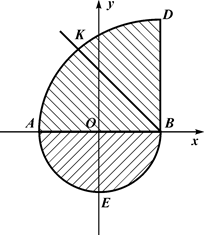
Приклад 7.4. Знайти координати центра ваги плоскої фігури, обмеженої півкругом 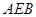 і четвертою частиною круга
і четвертою частиною круга 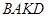 , якщо
, якщо  . Осі координат показані на рис. 7.32.
. Осі координат показані на рис. 7.32.
Розв’язання. Для розв’язання цієї задачі використаємо метод симетрії і метод розбиття.
7.4.1. Розіб’ємо дану плоску фігуру на дві частини: пів-
круг 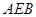 і круговий сектор
і круговий сектор 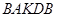 . Позначимо центри ваг цих частин і їх площі відповідно
. Позначимо центри ваг цих частин і їх площі відповідно 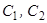 і
і 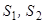 .
.
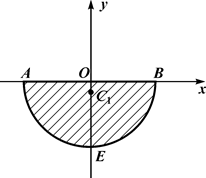
7.4.2. Центр ваги півкруга 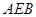 лежить на осі
лежить на осі 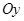 , за формулою наведеною в пункті 7.3.4:
, за формулою наведеною в пункті 7.3.4:
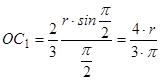 ,
,
тому 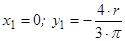 .
.
Площа півкруга дорівнює:
 .
.
 а)
а)
| |
 б)
б)
|
 в)
в)
|
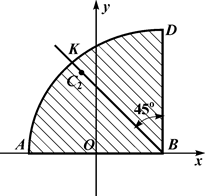
Рис. 7.32
7.4.3. Центр ваги  кругового сектора
кругового сектора 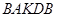 лежить на прямій
лежить на прямій 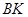 , за формулою наведеною в пункті 7.3.1.
, за формулою наведеною в пункті 7.3.1.
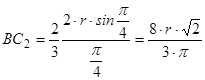 ,
,
тому
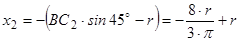 ;
;
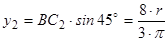 .
.
Площа кругового сектора дорівнює:
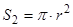 .
.
7.4.4. Координати центра ваги даної плоскої фігури 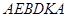 знаходимо за формулами (7.38):
знаходимо за формулами (7.38):
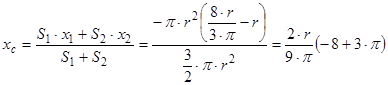 ;
;
 .
.
Відповідь: 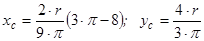
Приклад 7.5. Знайти координати центра ваги однорідної плоскої фігури, обмеженої гіперболою 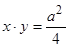 і прямими
і прямими 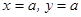 (рис. 7.33).
(рис. 7.33).
Розв’язання. Так як фігура АВЕ має вісь симетрії-бісектрису координатного кута, центр ваги лежить на цій бісектрисі. Таким чином, 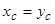 .
.
Для знаходження 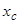 використаємо формулу
використаємо формулу
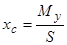 ,
,
де: 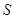 — площа фігури;
— площа фігури; 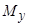 — статичний момент площі відносно осі
— статичний момент площі відносно осі 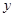 .
.
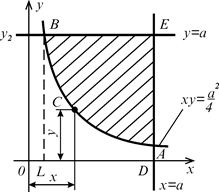
Рис. 7.33
Обидві ці величини вирахуємо з допомогою інтегрування.
7.5.1. Знайдемо абсциси крайніх точок фігури:
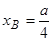 , (як точка перетину ліній
, (як точка перетину ліній 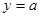 і
і 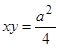 );
);
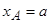 .
.
7.5.2. Площа плоскої фігури дорівнює:
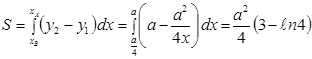 .
.
7.5.3. Статичний момент площі відносно осі 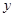 :
:
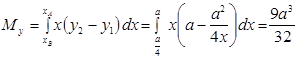 .
.
7.5.4. Координати центра ваги дорівнюють:
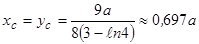 .
.
Відповідь: 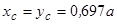 .
.
Приклад 7.6. Знайти координати центра ваги неоднорідного бруса у вигляді куба, в який запресований однорідний циліндр 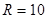 см (рис. 7.34). Питома вага бруса та циліндра відповідно дорівнюють
см (рис. 7.34). Питома вага бруса та циліндра відповідно дорівнюють
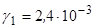 Н/см3 та
Н/см3 та 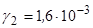 Н/см3.
Н/см3.
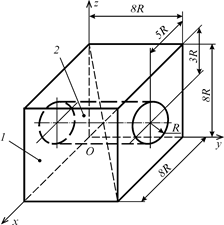
Рис. 7.34
Розв’язання. Для розв’язання використаємо метод розбиття та метод симетрії. Виділимо три тіла: брус у вигляді куба, висвердлений з нього циліндр із питомою вагою g1 і запресований циліндр із питомою вагою g2. Позначимо ваги бруса, запресованого в нього циліндра і висвердленого циліндра 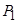 ,
, 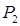 і
і 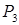 , центри їхніх ваг через -
, центри їхніх ваг через - 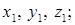
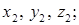
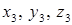 відповідно.
відповідно.
7.6.1. Сила ваги бруса в цілому:
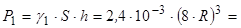
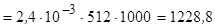 Н.
Н.
Координати центра ваги бруса дорівнюють:
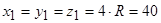 см.
см.
7.6.2. Сила ваги циліндричного стрижня дорівнює:
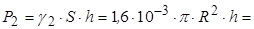
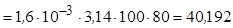 Н.
Н.
Координати центра ваги стрижня:
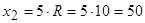 см;
см;
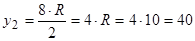 см;
см;
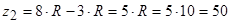 см.
см.
7.6.3. Сила ваги висвердленого циліндричного тіла радіусом 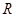 , дорівнює
, дорівнює
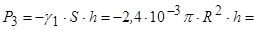
 Н.
Н.
Знак мінус, оскільки це тіло є висвердлене із бруса.
Координати центра ваги
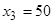 см;
см; 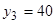 см;
см; 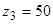 см.
см.
7.6.4. Знаходимо координати всього тіла за формулами:
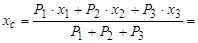
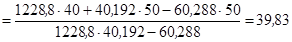 см
см
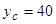 см, тому що тіло має площину симетрії, паралельну
см, тому що тіло має площину симетрії, паралельну 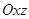 .
.
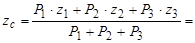
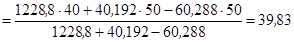 см
см
Відповідь: 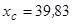 см;
см; 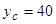 см;
см; 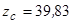 см.
см.