Задания по геометрии.

№1. Най­ди­те пло­щадь тре­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

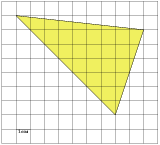
Ре­ше­ние. Пло­щадь тре­уголь­ни­ка равна раз­но­сти пло­ща­ди пря­мо­уголь­ни­ка и трех пря­мо­уголь­ных тре­уголь­ни­ков, ги­по­те­ну­зы ко­то­рых яв­ля­ют­ся сто­ро­на­ми ис­ход­но­го тре­уголь­ни­ка. По­это­му

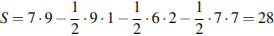см². Ответ: 28.

№2.

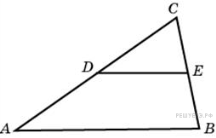Пло­щадь тре­уголь­ни­ка ABC равна 136. DE — сред­няя линия. Най­ди­те пло­щадь тре­уголь­ни­ка CDE.

Ре­ше­ние. Сред­няя линия тре­уголь­ни­ка от­се­ка­ет от него по­доб­ный тре­уголь­ник с ко­эф­фи­ци­ен­том 0, 5. Пло­ща­ди по­доб­ных фигур от­но­сят­ся как квад­рат ко­эф­фи­ци­ен­та по­до­бия, по­это­му пло­щадь от­се­чен­но­го тре­уголь­ни­ка вчет­ве­ро мень­ше пло­ща­ди ис­ход­но­го. Таким об­ра­зом, пло­щадь тре­уголь­ни­ка CDE равна 34.

Ответ: 34.

№3. Пло­щадь тре­уголь­ни­ка равна 217, а его пе­ри­метр 62. Най­ди­те ра­ди­ус впи­сан­ной окруж­но­сти.

Ре­ше­ние. Пло­щадь тре­уголь­ни­ка равна про­из­ве­де­нию по­лу­пе­ри­мет­ра на ра­ди­ус впи­сан­ной окруж­но­сти, по­это­му 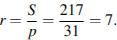Ответ: 7.

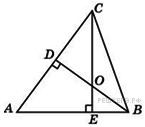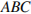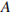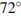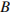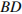№4. В тре­уголь­ни­ке угол равен , а углы и – ост­рые. и – вы­со­ты, пе­ре­се­ка­ю­щи­е­ся в точке . Най­ди­те угол 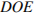. Ответ дайте в гра­ду­сах.

Ре­ше­ние. Cумма углов в вы­пук­лом че­ты­рех­уголь­ни­ке равна 360 гра­ду­сам, сле­до­ва­тель­но,

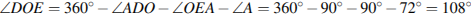. Ответ: 108.

№5.
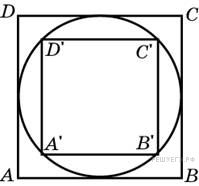Во сколь­ко раз пло­щадь квад­ра­та, опи­сан­но­го около окруж­но­сти, боль­ше пло­ща­ди квад­ра­та, впи­сан­но­го в эту окруж­ность? Ре­ше­ние.

Пусть ра­ди­ус окруж­но­сти равен R. Тогда сто­ро­на опи­сан­но­го во­круг нее квад­ра­та равна 2 R, а его пло­щадь, рав­ная квад­ра­ту сто­ро­ны, равна 4 R ². Диа­го­наль впи­сан­но­го квад­ра­та также равна 2 R, по­это­му его пло­щадь, рав­ная по­ло­ви­не про­из­ве­де­ния диа­го­на­лей, равна 2 R ². Сле­до­ва­тель­но, от­но­ше­ние пло­ща­ди опи­сан­но­го квад­ра­та к пло­ща­ди впи­сан­но­го равно 2. Ответ: 2.

№6. Две сто­ро­ны пря­мо­уголь­ни­ка 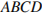равны 6 и 8. Най­ди­те длину век­то­ра .

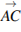Ре­ше­ние. Век­тор 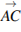об­ра­зу­ет в пря­мо­уголь­ни­ке два пря­мо­уголь­ных тре­уголь­ни­ка. По­это­му по тео­ре­ме Пи­фа­го­ра 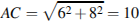. Ответ: 10.

№7.
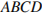Две сто­ро­ны пря­мо­уголь­ни­ка равны 6 и 8. Най­ди­те длину суммы век­то­ров 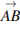и .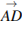

Ре­ше­ние. Сумма век­то­ров 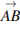и 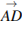равна век­то­ру 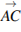. Век­тор 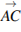об­ра­зу­ет в пря­мо­уголь­ни­ке два пря­мо­уголь­ных тре­уголь­ни­ка. По­это­му по тео­ре­ме Пи­фа­го­ра 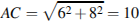. Ответ: 10.

№8.
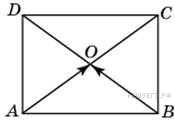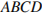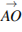Две сто­ро­ны изоб­ра­жен­но­го на ри­сун­ке пря­мо­уголь­ни­ка равны 6 и 8. Диа­го­на­ли пе­ре­се­ка­ют­ся в точке . Най­ди­те длину суммы век­то­ров и 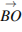. Ре­ше­ние. Сумма век­то­ров 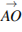и 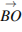равна век­то­ру 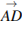. Его длина равна 6. Ответ: 6.

№9.
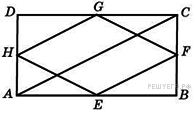Се­ре­ди­ны сто­рон пря­мо­уголь­ни­ка, диа­го­наль ко­то­ро­го равна 5, по­сле­до­ва­тель­но со­еди­не­ны от­рез­ка­ми. Най­ди­те пе­ри­метр об­ра­зо­вав­ше­го­ся че­ты­рех­уголь­ни­ка.

Ре­ше­ние. Че­ты­рех­уголь­ник 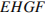ромб, зна­чит, его пе­ри­метр равен 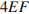. Сто­ро­ны ис­ко­мо­го че­ты­рех­уголь­ни­ка равны сред­ним ли­ни­ям тре­уголь­ни­ков, об­ра­зу­е­мых диа­го­на­ля­ми и сто­ро­на­ми дан­но­го че­ты­рех­уголь­ни­ка. Таким об­ра­зом, сто­ро­ны ис­ко­мо­го че­ты­рех­уголь­ни­ка равны по­ло­ви­нам диа­го­на­лей. Со­от­вет­ствен­но, имеем: 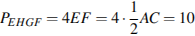. Ответ: 10.

№10.

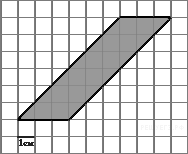Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.