Источники и классификация погрешностей

При замене задачи (1) на задачу (2) получаемое решение отличается от истинного решения задачи (1), т.е. несет в себе некоторую погрешность.

Погрешность решения задачи обуславливается следующими причинами:

1) математичское описание задачи является неточным, в частности, неточно заданы исходные данные описания;

2) применяемый для решения метод часто не является точным: получение точного решения возникающей математической задачи требует неограниченного или неприемлемо большого числа арифметических операций, поэтому вместо точного решения задачи приходится прибегать к приближенному;

3) при вводе данных в машину, при выполнении арифметических операций, при выводе данных производятся округления.

Погрешности, соответствующие этим причинам, называют:

1) неустранимой погрешностью;

2) погрешностью метода;

3) вычислительной погрешностью.

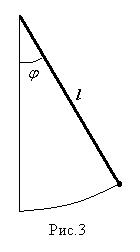Пример. Пусть имеется математический маятник (рис.3), который начинает свое движение в момент времени 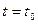. Требуется определить угол отклонения 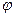от вертикали в момент .

Дифференциальное уравнение, описывающее колебание маятника, берется в виде:

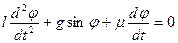, (3)

где 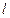- длина маятника, 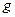- ускорение свободного падения, - коэффициент трения.

Как только принимается такое описание задачи, решение уже приобретает неустранимую погрешность, в частности, потому, что реальное трение зависит от скорости не совсем линейно; другой источник неустранимой погрешности состоит в погрешностях определения 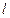, , 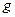, , , 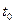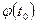. Название погрешности – «неустранимая» соответствует ее существу: она неконтролируема в процессе численного решения задачи и может уменьшится только за счет более точного описания физической задачи и более точного определения входных параметров. Дифференциальное уравнение (3) не решается в явном виде, для его решения требуется применить какой-нибудь численный метод. Вследствие этой причины возникает погрешность метода. Вычислительная погрешность возникает из-за конечности количества разрядов чисел, участвующих в вычислениях.

Введем формальные определения. Пусть 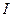- точное значение отыскиваемого параметра (в данном случае – реальный угол отклонения маятника 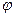в момент времени ), 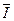- значение этого параметра, соответствующее принятому математическому описанию (математической модели) (в данном случае – значение 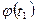точного решения уравнения (3)), 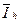- решение полученной математической задачи (в данном случае – уравнения (3)), получаемое при реализации численного метода в предположении отсутствия округлений, 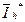- приближение к решению задачи, получаемое при реальных вычислениях. Тогда

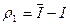- неустранимая погрешность,

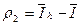- погрешность метода,

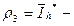
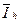- вычислительная погрешность,

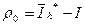- полная погрешность.

Полная погрешность удовлетворяет равенству

.

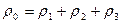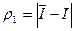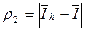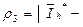
Возможно полагать , , 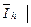. В таких обозначениях .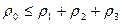