Абсолютная и относительная погрешности

Пусть 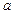- точное значение некоторой скалярной величины, а 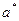- известное приближение к нему. Тогда абсолютной погрешностью приближенного значения 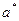называется 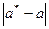, а относительной - 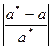. Однако чаще всего точное значение 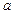неизвестно, поэтому далее под абсолютной (относительной) погрешностью будем понимать некоторую величину 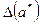(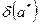), про которую известно, что

.

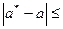
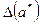
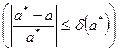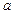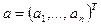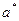Если - точное значение не скалярной, а векторной величины, т.е. , а - известное приближение к нему: 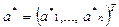, то, по аналогии со скалярной величиной, под абсолютной (относительной) погрешностью будем понимать некоторую величину 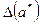(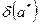), про которую известно, что

,

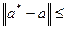
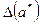
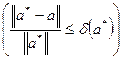где 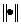- норма вектора-аргумента.

Если 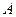- матрица, а 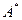- матрица приближения, то под абсолютной (относительной) погрешностью будем понимать некоторую величину 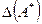(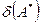), про которую известно, что

,

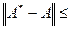
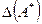
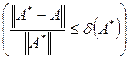где 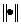- матричная норма.

Относительную погрешность часто выражают в процентах.

Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой слева.

Пример. У чисел 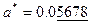, 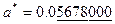значащие цифры подчеркнуты.

Значащую цифру называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.

Пример. 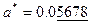, 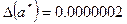; 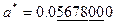, 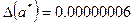. Подчеркнутые цифры – верные.

Если все значащие цифры верные, то говорят, что число записано со всеми верными цифрами.

Часто информация о некоторой величине задается пределами ее измерения:

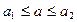(например, ).

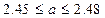Принято записывать эти пределы с одинаковым числом знаков после запятой.

Информация о том, что 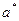является приближенным значение числа 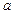с абсолютной погрешностью 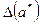, иногда записывают в виде

,

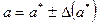числа 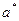и 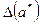принято записывать с одинаковым числом знаков после запятой. Например,

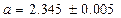
означает, что

.

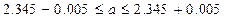Соответственно информацию о том, что 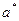является приближенным значение числа 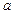с относительной погрешностью 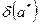, записывают в виде:

.

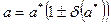Например, запись

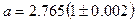
означает, что

.

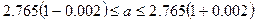Следует различать формально математическую и обиходную терминологии в рассуждении о величине погрешности. Если в постановке задачи говорится, что требуется найти решение с погрешностью 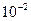, то чаще всего предполагается лишь, что погрешность имеет такой порядок. Если, например, решение будет найдено с погрешностью 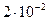, то такой результат, скорее всего, также удовлетворит заказчика.