Квадратурная формула трапеций. Геометрический смысл составной квадратурной формулы трапеций

Лекция 16. Численное интегрирование

План

Задача численного интегрирования. Основная идея численного интегрирования

Качественная оценка погрешности численного интегрирования

Понятие квадратурной формулы, составной квадратурной формулы

Квадратурная формула прямоугольников. Геометрический смысл составной квадратурной формулы прямоугольников

Квадратурная формула трапеций. Геометрический смысл составной квадратурной формулы трапеций

1. Задача численного интегрирования. Основная идея численного интегрирования

К приближенному вычислению значения интеграла 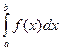приходится прибегать, если не удается найти первообразную 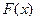для подинтегральной функции 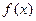, выраженную через элементарные функции, или поиск этой первообразной по каким-либо причинам затруднен, но искомый интеграл существует.

Хотя из определения 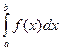следут, что с помощью интегральной суммы 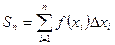можно найти интеграл с любой степенью точности, но этот прием замены интеграла интегральной суммой практически мало используется из-за недостаточно быстрой сходимости .

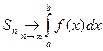Основная идея численного (приближенного) интегрирования заключается в следующем. Для построения формул приближенного вычисления 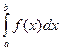используется замена функции 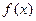интерполирующей функцией :

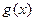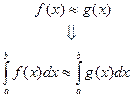(5)

1. Качественная оценка погрешности численного интегрирования

Замена подинтегральной функции 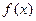интерполирующей функцией 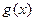естественно приводит к погрешности при вычислении интеграла. Возникает вопрос: если предположить, что интерполянт 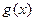достаточно точно приближает функцию 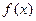на всем сегменте интегрирования 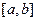, т.е. 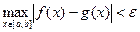, где 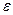- мало, что можно сказать о погрешности вычисления самого интеграла, т.е. о величине 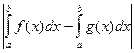? При детальном ее рассмотрении получим:

.

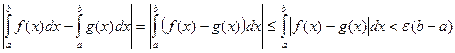Таким образом, если мала погрешность при замене 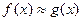, то малой будет и погрешность приближенного значения интеграла 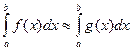. Численное интегрирование (в отличие от численного дифференцирования, как будет показано в последующих лекциях) обычно «сглаживает» и уменьшает погрешность, допущенную при первоначальной замене входных данных ().

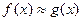1. Понятие квадратурной формулы, составной квадратурной формулы

Для численного приближения определенных интегралов используется понятие квадратуры.

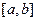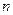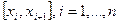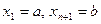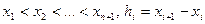Пусть сегмент интегрирования разбит на частей – частичных (или элементарных) сегментов , и . Функция 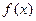определена и интегрируема на 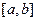. Необходимо вычислить 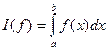. Обозначим

,

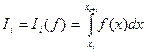Тогда

.

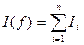Определение 1. Квадратурной формулой называется формула, аппроксимирующая (приближающая) отдельный интеграл 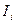на частичном сегменте. Составная квадратурная формула – это формула, дающая приближение к 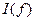в виде суммы приближений по данной квадратурной формуле к отдельным интегралам .

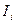Двумя простейшими квадратурными формулами являются формула прямоугольников и формула трапеций.

1. Квадратурная формула прямоугольников. Геометрический смысл составной квадратурной формулы прямоугольников

Квадратурная формула средних прямоугольников использует значения функции 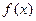в средних точках элементарных отрезков:

.

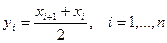Квадратурная формула средних прямоугольников аппроксимирует каждый интеграл 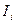значением площади прямоугольника с основанием 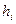и высотой :

,

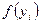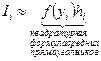тогда составная квадратурная формула средних прямоугольников будет иметь вид:

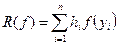, (7)

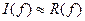. (10)

Геометрическая интерпретация формулы (10) представлена на рис.1.

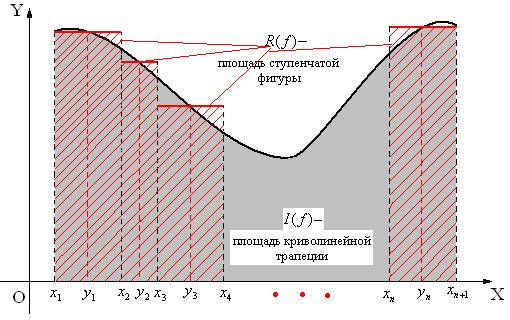
Рис.1.

Следуя формуле (5), составную квадратурную формулу (7) мы бы получили при замене подинтегральной функции 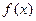в 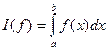на интерполяционный сплайн нулевой степени.

Существуют также квадратурные формулы левых (правых) прямоугольников:

.

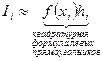
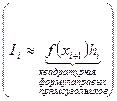Соответствующие составные квадратурные формулы левых (правых) прямоугольников имеют вид:

.

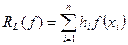
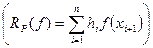1. Квадратурная формула трапеций. Геометрический смысл составной квадратурной формулы трапеций

Квадратурная формула трапеций использует значения функции в концевых точках элементарных отрезков:

.

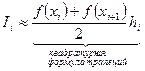Соответственно составная квадратурная формула трапеций имеет вид:

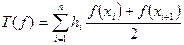. (15)

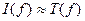. (20)

Геометрическая интерпретация формулы (20) представлена на рис.2.

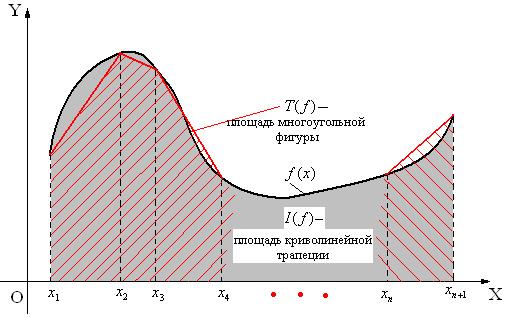
Рис.2.

Следуя формуле (5), составную квадратурную формулу (15) мы бы получили при замене подинтегральной функции 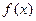в 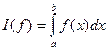на интерполяционный сплайн первой степени.

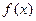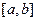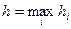Если функция интегрируема по Риману на , а , то

, .

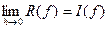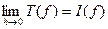Вопросы

1. В каком случае приходится прибегать к численному интегрированию?
2. Основная идея численного интегрирования.
3. Что происходит с погрешностью, допущенной при аппроксимации входных данных при численном интегрировании?
4. Что такое квадратурная формула, составная квадратурная формула?
5. Квадратурная, составная квадратурная формула левых, правых, средних прямоугольников. Геометрический смысл этих формул.
6. Какая интерполирующая функция используется для подинтегральной функции 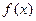при получении составных квадратурных формул прямоугольников?
7. Квадратурная формула трапеций. Геометрический смысл составной квадратурной формулы трапеций.
8. Какая интерполирующая функция используется для подинтегральной функции 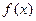при получении составной квадратурной формулы трапеций?