Принцип Рунге оценки погрешности численного интегрирования

Лекция 17. Погрешность численного интегрирования

План

Вывод погрешности формулы средних прямоугольников на элементарном отрезке.

Вывод погрешности формулы трапеций на элементарном отрезке.

Сравнение точностей различных квадратурных формул. Квадратурная формула Симпсона

Принцип Рунге оценки погрешности численного интегрирования

1. Вывод погрешности формулы средних прямоугольников на элементарном отрезке

Составная квадратурная формула средних прямоугольников для численного вычисления интеграла Римана 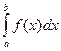основана на кусочно-постоянной интерполяции (подинтегральная функция заменяется на интерполяционный сплайн нулевой степени), формула трапеций использует кусочно-линейную интерполяцию (подинтегральная функция заменяется на интерполяционный сплайн первой степени). Возникает вопрос: какая из квадратурных формул точнее?

Предположим, что подинтегральная функция 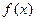имеет непрерывные производные до 5-го порядка включительно, и значения этих производных на 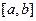не слишком велики. Рассмотрим элементарный отрезок 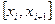. Разложение по формуле Тейлора с остаточным членом в форме Пеано для 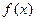относительно центра этого элементарного отрезка 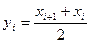имеет вид:

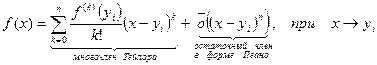(5)

т.е.

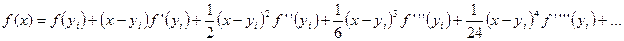(11)

Предположения относительно 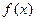означают, что остаточный член, обозначенный многоточием, по величине меньше явно выписанных членов.

Проинтегрируем равенство (11) на элементарном отрезке :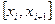

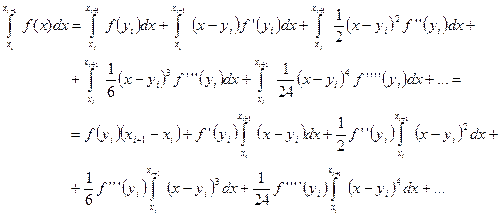(15)

Как видно, вычисление 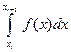в итоге свелось к вычислению интегралов вида 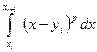при различных значениях показателя степени 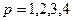. Для удобства дальнейших вычислений рассмотрим этот интеграл отдельно:

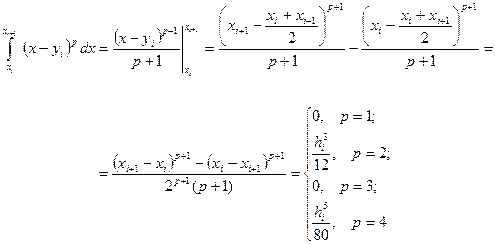(18)

где .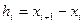

Подставляя (18) в (15), получим

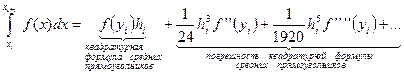(20)

Формула (20) дает точную формулу погрешности квадратурной формулы средних прямоугольников. Когда 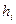мало, ошибка квадратурной формулы средних прямоугольников на элементарном отрезке 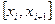- это

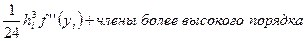. (25)

Первое слагаемое дает основной вклад в значение погрещности, т.к. все остальные члены значительно меньше первого (в предположении, что 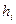мало).

1. Вывод погрешности формулы трапеций на элементарном отрезке

Вернемся к разложению Тейлора (11), подставляя туда сначала 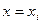, а затем :

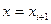(30)

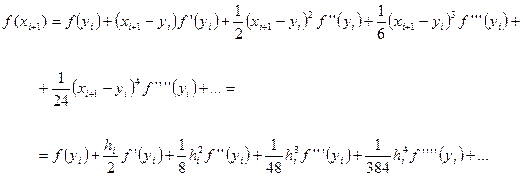(40)

Сложим почленно формулы (30) и (40), результат поделим на 2:

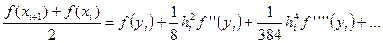(50)

Из (50) выразим :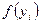

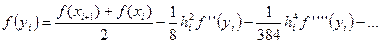
и подставим полученное выражение в (20):

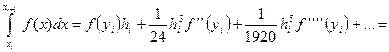
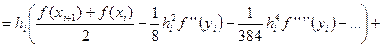
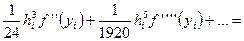
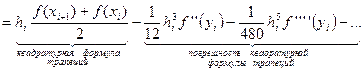
Таким образом, ошибка квадратурной формулы трапеции на элементарном отрезке равна

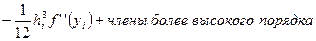. (55)

1. Сравнение точностей различных квадратурных формул. Квадратурная формула Симпсона

Общая ошибка каждой из составных квадратурных формул есть сумма ошибок на отдельных элементарных отрезках. Пусть

, .

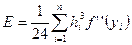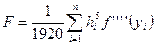Тогда

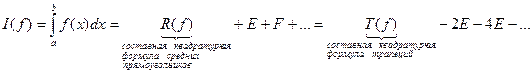(60)

где

, .

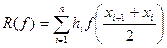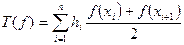Если 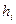достаточно малы, то 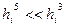, и если 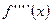ограничена, то 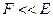, откуда следует, что для многих функций 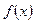квадратурная формула средних прямоугольников примерно вдвое точнее формулы трапеций.

Замечание. Квадратурные формулы средних прямоугольников и трапеций точны для многочленов первой степени.

Предположим, что для 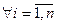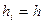. Оценим в этом случае погрешность 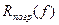составной квадратурной формулы средних прямоугольников, учитывая только самый главный член этой погрешности :

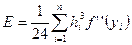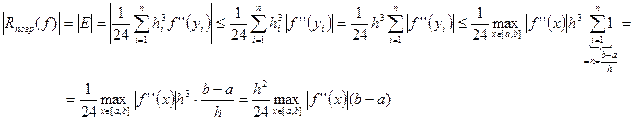(61)

Аналогичная оценка погрешности 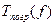в случае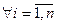 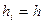для составной квадратурной формулы трапеций даст

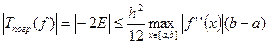. (62)

Из (60) получаем:

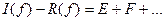(65)

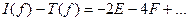(70)

Умножим (65) на 2/3, а (70) на 1/3 и результаты сложим:

______________________________

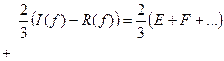
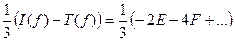
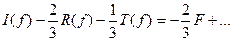(80)

Обозначим:

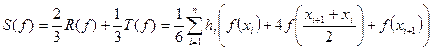. (90)

Формула (90) – составная квадратурная формула Симпсона. С учетом (90) формулу (80) можно записать в виде:

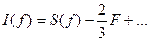
Тогда погрешность формулы Симпсона будет равна:

, (100)

Откуда вытекает, что формула Симпсона является более точной, чем формулы прямоугольников и трапеций, в частности, эта формула, как следует из (100), вообще не дает погрешности при интегрировании многочленов до третьей степени включительно.

Оценим погрешность 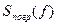составной квадратурной формулы Симпсона в случае 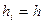для 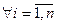, учитывая только самый главный член этой погрешности :

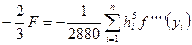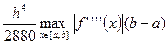. (105)

Формулы (61), (62), (105) позволяют оценить порядок точности 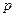квадратур по отношению к шагу 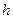(это показатель степени при 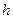). Для формул средних прямоугольников и трапеций , для формулы Симпсона .

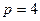1. Принцип Рунге оценки погрешности численного интегрирования

На практике чаще всего приходится решать следующую задачу: известна погрешность, с которой требуется вычислить интеграл, необходимо выбрать соответствующий шаг интегрирования для достижения указанной точности. Один из методов решения этой задачи – принцип Рунге, основан на двойном пересчете.

Пусть для вычисления интеграла

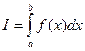
применяется одна из квадратурных формул с шагом 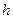. Предположим, что известен порядок точности 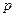применяемой формулы. Обозначим 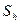приближенное решение, полученное по этой формуле с шагом 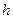, а 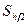- с шагом 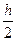. Тогда

.

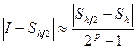Для достижения заданной точности 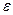при вычислении интеграла задается некоторый шаг 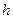, рассчитывается 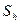, затем, последовательно уменьшая шаг в 2 раза, вычисляется 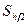до тех пор, пока не будет выполняться соотношение

.

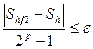В этом случае полагают

.

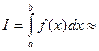
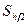Вопросы

1. Погрешность формулы средних прямоугольников на элементарном отрезке.
2. Погрешность формулы трапеций на элементарном отрезке.
3. Какая из квадратурных формул трапеций и средних прямоугольников точнее? Почему?
4. Формула Симпсона, ее связь с квадратурными формулами прямоугольников и трапеций.
5. Порядок точности формулы.
6. Для каких функций не дает погрешности квадратурная формула трапеций, средних прямоугольников, Симпсона? Почему?
7. Метод Рунге оцнки погрешности численного интегрирования.