
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Две задачи, на которые распадается задача решения нелинейного уравнения. Задача отделения корней нелинейного уравнения и методы ее решения
|
|
Задача решения нелинейного уравнения (1) распадается на две подзадачи:
1) Отделение корней – определение интервалов, в каждом из которых лежит только один корень уравнения (1);
2) Непосредственное вычисление корней с заданной точностью.
Первая задача является наиболее сложной. Для ее решения чаще применяются графический метод, а также методы, основанные на математическом анализе (вторые служат для уточнения результата, полученного графическим методом).
При использовании графического метода возможны два варианта.
Во-первых, достаточно построить график функции 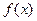 и определить точки пересечения графика с осью ОХ. Тогда интервалы, содержащие эти точки, и будут результатами решения задачи отделения корней. Например, пусть требуется решить нелинейное уравнение:
и определить точки пересечения графика с осью ОХ. Тогда интервалы, содержащие эти точки, и будут результатами решения задачи отделения корней. Например, пусть требуется решить нелинейное уравнение:
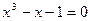 .
.
Здесь 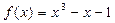 . График этой функции представлен на рис.1. Из графика видно, что рассматриваемое уравнение имеет единственный вещественный корень
. График этой функции представлен на рис.1. Из графика видно, что рассматриваемое уравнение имеет единственный вещественный корень 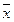 , который находится между 1 и 2. Таким образом, результатом отделения корней является единственный интервал
, который находится между 1 и 2. Таким образом, результатом отделения корней является единственный интервал  .
.
Если функция 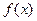 имеет достаточно сложное представление (а потому и построение ее графика вызывает затруднение), можно использовать графический метод в другом варианте. Исходное уравнение
имеет достаточно сложное представление (а потому и построение ее графика вызывает затруднение), можно использовать графический метод в другом варианте. Исходное уравнение  представляется в эквивалентном виде:
представляется в эквивалентном виде:
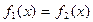 ,
,
для которого функции 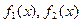 имеют менее сложное представление, чем
имеют менее сложное представление, чем 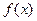 . Тогда для отделения корней в одной системе координат строятся графики функций
. Тогда для отделения корней в одной системе координат строятся графики функций 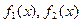 . Решение уравнения – это абсцисса точки пересечения построенных графиков.
. Решение уравнения – это абсцисса точки пересечения построенных графиков.
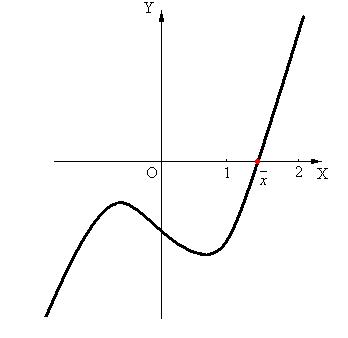
Рис.1.
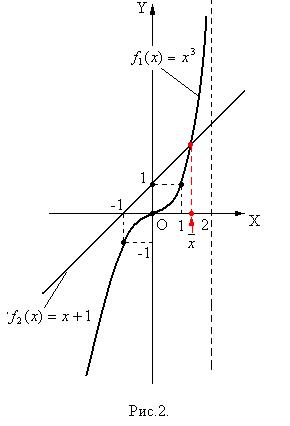
Для предыдущего примера уравнение 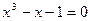 можно представить в эквивалентном виде:
можно представить в эквивалентном виде: 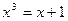 , где
, где 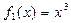 ,
, 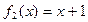 , тогда отделение корня
, тогда отделение корня 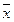 приводит к тому же результату – это
приводит к тому же результату – это  (рис.2).
(рис.2).
Проверим, насколько правильно отделен корень уравнения 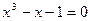 , используя теоремы математического анализа. Характер монотонности функции
, используя теоремы математического анализа. Характер монотонности функции 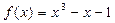 определяется знаком ее производной. Поскольку
определяется знаком ее производной. Поскольку 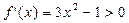 при
при 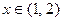 , то
, то 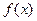 строго монотонно возрастает на
строго монотонно возрастает на  и значит ее график может пересечь ось ОХ не более одного раза (может не пересечь вовсе). Поскольку на концах
и значит ее график может пересечь ось ОХ не более одного раза (может не пересечь вовсе). Поскольку на концах 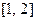 непрерывная функция
непрерывная функция 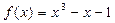 принимает значения разных знаков (
принимает значения разных знаков (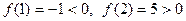 ), то по теореме Ролля ее график обязательно пересекает ось ОХ (единственный раз в силу строгой монотонности функции). Таким образом,
), то по теореме Ролля ее график обязательно пересекает ось ОХ (единственный раз в силу строгой монотонности функции). Таким образом,  действительно содержит единственный корень уравнения, отделение проведено верно.
действительно содержит единственный корень уравнения, отделение проведено верно.
Таким образом, для уточнения правильности отделения корня нелинейного уравнения, проведенного графическим методом, в общем случае достаточно проверить следующие условия. Пусть при графическом отделении корней уравнения 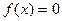 установлено, что
установлено, что 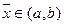 . Тогда, если:
. Тогда, если:
1. 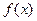 строго монотонна на
строго монотонна на 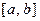 ;
;
2. 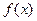 непрерывна на
непрерывна на 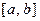 ;
;
3. 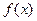 на концах сегмента
на концах сегмента 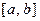 принимает значения разных знаков:
принимает значения разных знаков: 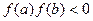 ,
,
 то при одновременном выполнении всех трех условий можно утверждать, что
то при одновременном выполнении всех трех условий можно утверждать, что 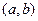 действительно содержит корень уравнения
действительно содержит корень уравнения 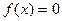 , и этот корень единственный, т.е. графический метод дал правильное отделение корня.
, и этот корень единственный, т.е. графический метод дал правильное отделение корня.
Необходимо отметить, что каждое из условий 1-3 являются достаточными, но не необходимыми, т.е. даже при невыполнении этих условий 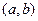 может быть найден верно, т.е. содержать единственный корень уравнения (рис.3). Так функция, график которой представлен на рис.3(а), не является строго монотонной на
может быть найден верно, т.е. содержать единственный корень уравнения (рис.3). Так функция, график которой представлен на рис.3(а), не является строго монотонной на 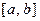 ; функция, отвечающая графику на рис.3(б), не является непрерывной на
; функция, отвечающая графику на рис.3(б), не является непрерывной на 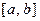 ; а для графика 3(в) не выполняется условия различия знаков значений функции на концах
; а для графика 3(в) не выполняется условия различия знаков значений функции на концах 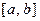 , но в каждом из этих трех случаев корень уравнения был отделен верно.
, но в каждом из этих трех случаев корень уравнения был отделен верно.
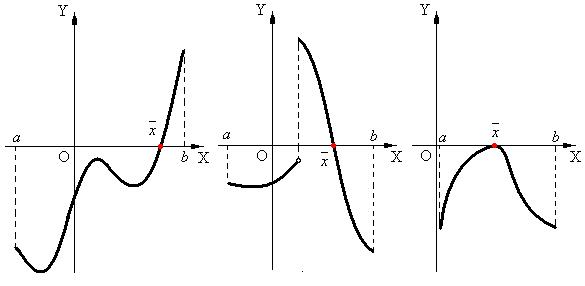
Очень часто на практике выполнение условия различия знаков значений функции 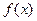 на концах
на концах 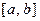 без учета других свойств функции
без учета других свойств функции 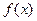 принимается за достаточное условие того, что
принимается за достаточное условие того, что 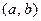 содержит единственный корень уравнения
содержит единственный корень уравнения 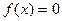 , что часто не соответствует действительности (рис.4). Только одновременное выполнение условий 1-3 является достаточным подтверждением правильности отделения корня нелинейного уравнения.
, что часто не соответствует действительности (рис.4). Только одновременное выполнение условий 1-3 является достаточным подтверждением правильности отделения корня нелинейного уравнения.
а б в
Рис.3.
Рис.4.
Замечание 1. Пусть функция 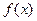 из уравнения (1) непрерывна и изменяет знак на
из уравнения (1) непрерывна и изменяет знак на 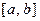 . Значения переменной
. Значения переменной 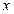 и вычисляемые значения
и вычисляемые значения 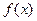 - это числа с плавающей точкой, представимые в машине, т.е. как сама переменная
- это числа с плавающей точкой, представимые в машине, т.е. как сама переменная 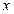 , так и
, так и 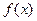 могут принимать значния из дискретного конечного множества, среди которых в силу вычислительной погрешности может не оказаться нуля. Поэтому при решении уравнения
могут принимать значния из дискретного конечного множества, среди которых в силу вычислительной погрешности может не оказаться нуля. Поэтому при решении уравнения 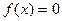 бó льший смысл имеет искать не нуль функции
бó льший смысл имеет искать не нуль функции 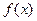 (он может не существовать в используемой системе с плавающей точкой), а малый по длине интервал
(он может не существовать в используемой системе с плавающей точкой), а малый по длине интервал 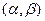 , в котором
, в котором 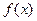 меняет знак. Такой интервал всегда можно найти и можно сузить его настолько, насколько позволяет система чисел с плавающей точкой, т.е. так, чтобы концевыми точками интервала были два соседних числа этой системы. Для этого можно использовать мтод деления отрезка пополам.
меняет знак. Такой интервал всегда можно найти и можно сузить его настолько, насколько позволяет система чисел с плавающей точкой, т.е. так, чтобы концевыми точками интервала были два соседних числа этой системы. Для этого можно использовать мтод деления отрезка пополам.