Метод деления отрезка пополам, его особенности, недостатки. Скорость сходимости метода деления отрезка пополам

Метод деления отрезка пополам – один из наиболее часто используемых численных методов для решения нелинейных уравнений.

Пусть результатом отделения очередного вещественного корня уравнения (1) является интервал 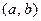, корень уравнения требуется вычислить с точностью .

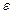При заданной точности 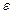метод состоит в следующем:

1. Положить 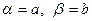. Вычислить ;

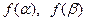2. Положить 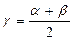, вычислить ;

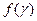3. Если 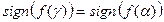, то 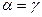; иначе ;

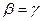4. Проверка достижения заданной точности. Если 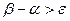, то переход на шаг 2 (на следующую итерацию метода); иначе 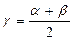- искомый корень.

К достоинствам метода деления отрезка пополам следует отнести его надежность (или гарантированную сходимость): если первоначально корень был отделен верно, т.е. 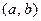действительно содержал единственный корень уравнения (1), то он обязательно будет найден с заданной точностью.

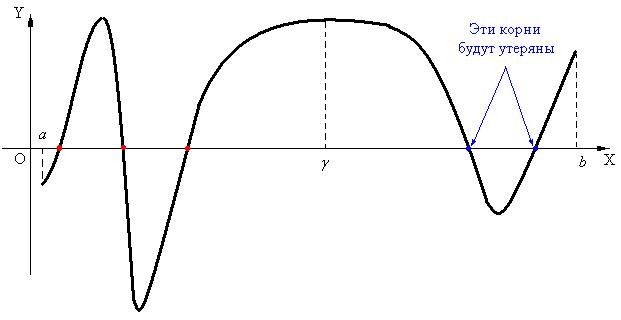
Рис.5.

Главным недостатком метода является то, что если 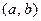на самом деле содержал более одно вещественного корня уравнения (1) (корень был отделен не верно на первом этапе решения уравнения), то в ходе решения произойдет потеря всех корней, кроме одного (рис.5 – отмеченные на рисунке корни будут утеряны уже на первой итерации).

Недостатком метода деления отрезка пополам также является его медленная сходимость: погрешность приближения к решению уравнения от шага к шагу уменьшается лишь в два раза.

Вопросы

1. Общий вид нелинейного уравнения.
2. На какие две задачи распадается задача решения нелинейного уравнения?
3. Что значит отделить корень нелинейного уравнения?
4. Какие методы отделения корней нелинейного уравнения используются на практике?
5. Как можно уточнить интервал, полученный после отделения корня нелинейного уравнения?
6. К чему приводят особенности машинной арифметики при решении нелинейного уравнения?
7. Основное достоинство метода деления отрезка пополам для решения елинейного уравнения.
8. Недостатки метода деления отрезка пополам.