Задачи, приводящие к вычислению собственных значений

Решение многих задач физики, химии, астрономии, строительства и т.д. сводится к задаче вычисления собственных значений и собственных векторов соответствующих матриц.

Если ставится задача отыскания всех собственных значений и собственных векторов матрицы, то она называется полной проблемой собственных значений. Если при решении задачи требуются лишь какие-то из собственных значений и собственных векторов анализируемой матрицы, то такие задачи называются частичными проблемами собственных значений.

К частичным проблемам собственных значений приводят следующие задачи:

· При изучении и анализе модели атомного ядра в физике требуются оценки для наименьшего и наибольшего по модулю собственных значений некоторой матрицы ;

· При изучении и рассчете строительных конструкций возникает задача вычисления двух или нескольких собственных значений некоторой матрицы, максимальных по модулю;

· Задача рассчета устойчивости строительных конструкций приводит к задаче вычисления собственного значения некоторой матрицы, ближайшего к заданному значению .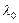

Обычно все задачи при решении частичных проблем собственных значений сводятся к вычислению максимального по модулю собственного значения.

Формально расуждая, можно было бы сказать, что частичные проблемы собственных значений являются частными случаями полной проблемы и достаточно ограничиться рассмотрением методов решения именно полной проблемы мсобственных значений. Однако такой подход приведет к неоправданно большому объему вычислений. При обсуждении постановок конкретных задач, связанных с отысканием собственных значений матриц, зчастую значительные усилия тратятся именно на установление минимального объема информации о спектре матрицы, которым можно ограничиться.