Подобное преобразование матрицы, его свойства

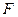Определение 4. Пусть - данная матрица, - невырожденная матрица. Тогда преобразование

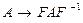
называется подобным преобразованием матрицы .

Подобное преобразование играет огромную роль в процессе решения задач на собственные значения в силу следующего свойства.

Теорема. Пусть матрица 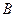получена путем подобного преобразования матрицы , т.е. 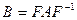. Если 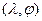- собственная пара матрицы , то - собственная пара 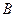. Иными словами: подобное преобразование не меняет спектр матрицы.

Доказательство. Рассмотрим характеристический многочлен для матрицы :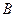

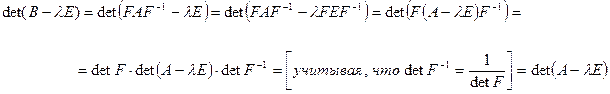
т.е. характеристические многочлены матриц 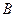и совпадают, а значит совпадают характеристические уравнения, а следовательно, совпадают и спектры: собственные значения у матриц 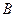и одинаковые.

Пусть теперь 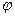- собственный вектор матрицы , отвечающий собственному значению 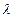. Это означает, что 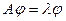. По доказаному выше 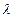- это собственное значение и матрицы 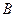, а значит существует собственный вектор матрицы 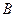, отвечающий 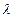, т.е. такой, что: .

.

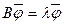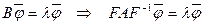Умножим обе части последнего равенства на матрицу 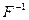слева. Получим:

,

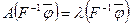т.е. вектор 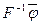- собственный вектор матрицы . Зная, что 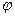- собственный вектор матрицы , а значит, и 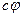для любого 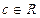, получаем, что

,

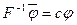откуда после умножения обеих частей на матрицу 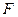слева получаем:

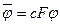
собственный вектор матрицы 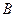. При 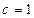получаем: 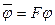, что и требовалось доказать.