
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Преобразование отражения. Сведение матрицы к почти треугольному виду
|
|
Запишем 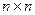 -матрицу
-матрицу 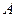 в виде:
в виде:
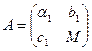 ,
,
где 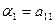 ,
, 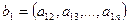 ,
, 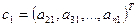 .
.
Построим матрицу отражения:
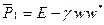 ,
,
где  ,
, 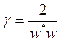 . Матрица
. Матрица 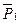 - самосопряженная и ортогональная. Действительно:
- самосопряженная и ортогональная. Действительно:
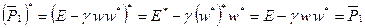 ;
;
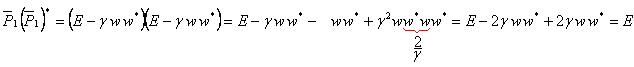
Построим матрицу
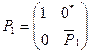 .
.
В силу свойств матрицы 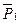 матрица
матрица 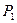 также является самосопряженной и ортогональной.
также является самосопряженной и ортогональной.
Рассмотрим:
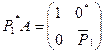
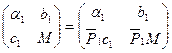 .
.
Рассмотрим подробнее элементы матрицы 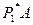 :
:
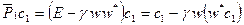 , (1)
, (1)
при этом
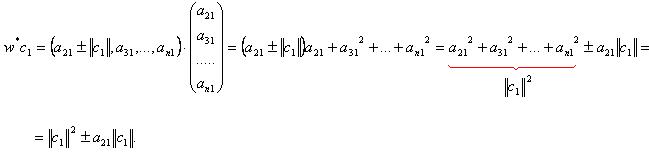
Уточним выражение для 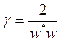 . Для этого вычислим
. Для этого вычислим 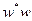 :
:
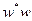
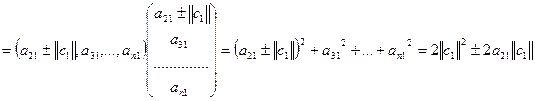 ,
,
тогда
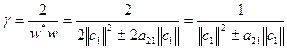 .
.
Возвращаясь к формуле (1), вычислим
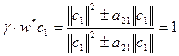 ,
,
поэтому
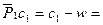
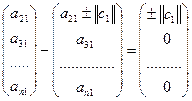 .
.
Таким образом, у матрицы 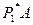 нули в первом столбце, начиная с третьего элемента.
нули в первом столбце, начиная с третьего элемента.
Для сохранения подобия необходимо матрицу 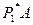 умножить на
умножить на 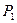 справа:
справа:
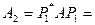
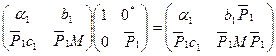 .
.
Очевидно, первый столбец матрицы остался без изменений.
Далее строится матрица отражения для второго столбца матрицы 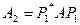 для получения нулей во втором столбце преобразованной матрицы, начиная с четвертого элемента и т.д. Конечный результат – построение верхней почти треугольной матрицы.
для получения нулей во втором столбце преобразованной матрицы, начиная с четвертого элемента и т.д. Конечный результат – построение верхней почти треугольной матрицы.
Вопросы
- На чем принципиально основаны методы решения полной проблемы собственных значений?
- Основные шаги общей схемы решения полной проблемы собственных значений.
- Какая матрица называется верхней (нижней) почти треугольной?
- Какая матрица называется трехдиагональной?
- Что такое матрица Якоби?
- Как определяется спектр разложимой матрицы?
- Что характерно для собственных значений матрицы Якоби?
- Для чего используется матрица отражения?
- Свойства матрицы отражения.
.