
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема об LU-разложении матрицы
|
|
Рассматривается неоднородная система линейных алгебраических уравнений (СЛАУ):
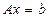 , (5)
, (5)
где 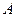 -
- 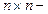 матрица системы,
матрица системы, 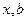 - вектор неизвестных и правой части соответственно,
- вектор неизвестных и правой части соответственно, 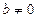 .
.
Теорема. Пусть все ведущие подматрицы 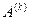 ,
, 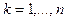 , матрицы
, матрицы 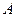 являются невырожденными. Тогда
являются невырожденными. Тогда 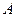 единственным образом представима в виде:
единственным образом представима в виде:
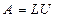 , (10)
, (10)
где 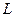 - нижняя треугольная матрица с единицами на главной диагонали,
- нижняя треугольная матрица с единицами на главной диагонали, 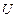 - верхняя треугольная матрица, диагональные элементы которой определяются по формуле:
- верхняя треугольная матрица, диагональные элементы которой определяются по формуле:
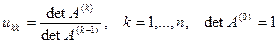 . (15)
. (15)
Представление (10) называется LU-разложением матрицы 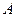 .
.
Доказательство. Доказательство проведем конструктивно, т.е. построим непосредственно разложение (10). Напомним, что главные подматрицы 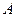 - это
- это

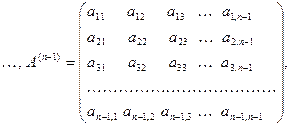
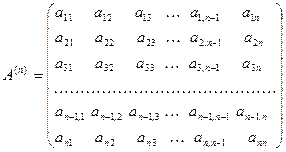 .
.
Предположим, что разложение (10) уже построено, т.е. матрица 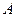 представлена в виде:
представлена в виде:
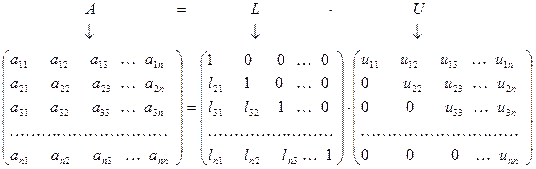
Элементы матрицы 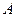 известны, а элементы матриц
известны, а элементы матриц 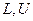 необходимо найти. Построим систему уравнений относительно неизвестных элементов матриц
необходимо найти. Построим систему уравнений относительно неизвестных элементов матриц 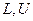 , записывая уравнения для соответствующих элементов матрицы
, записывая уравнения для соответствующих элементов матрицы 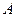 :
:
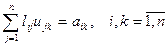 (20)
(20)
или, учитывая, что
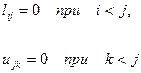
систему (20) можно записать в виде:
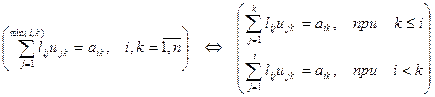 . (22)
. (22)
Записывая последовательно уравнения системы (20), получим:
для 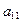 , учитывая, что этот элемент получается при умножении первой строки матрицы
, учитывая, что этот элемент получается при умножении первой строки матрицы 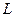 на первый столбец матрицы
на первый столбец матрицы 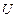 :
:
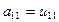 ,
,
откуда сразу получаем значение для 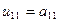 .
.
Элемент 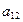 получается как результат умножения первой строки матрицы
получается как результат умножения первой строки матрицы 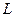 на второй столбец матрицы
на второй столбец матрицы 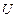 :
:
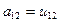 ,
,
откуда  .
.
Идя последовательно по элементам первой строки матрицы 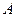 , получим, что
, получим, что
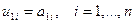 .
.
Переходим на вторую строку матрицы 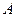 :
:
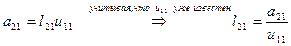 .
.
 ,
,
и т.д. Проводя вычисления, составляя уравнения для элементов матрицы 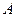 в порядке
в порядке
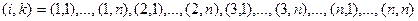 ,
,
получим следующие формулы для вычисления неизвестных элементов матриц 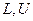 :
:
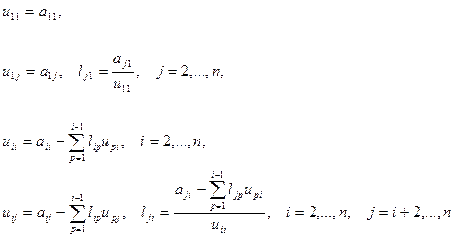 (25)
(25)
Ясно, что вычисления по формулам (25) можно вести только тогда, когда  . Проверим выполнение этого условия. Из (22) следует, что
. Проверим выполнение этого условия. Из (22) следует, что
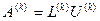 ,
,
поэтому
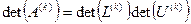 . (30)
. (30)
Поскольку 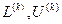 нижняя и верхняя треугольные матрицы соответственно, то их определители равны произведению элементов, стоящих на главной диагонали, поэтому
нижняя и верхняя треугольные матрицы соответственно, то их определители равны произведению элементов, стоящих на главной диагонали, поэтому
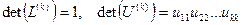 ,
,
и, как следует из (30)
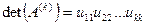 .
.
По условию теоремы все 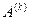 ,
, 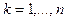 невырожденные, т.е.
невырожденные, т.е.
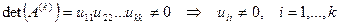 ,
,
кроме того 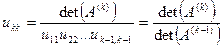 ,
,
что и требовалось доказать.