
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
СЛАУ с симметричными положительно определенными матрицами. Метод Холесского
|
|
Пусть матрица СЛАУ (5) симметричная и положительно определенная, т.е.: 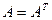 и для любого ненулевого вектора
и для любого ненулевого вектора 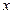 соответствующей размерности
соответствующей размерности 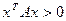 . Поскольку для положительно определенной матрицы выполняется критерий Сильвестра, то определители всех главных подматриц матрицы
. Поскольку для положительно определенной матрицы выполняется критерий Сильвестра, то определители всех главных подматриц матрицы 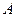 не равны нулю (они строго больше нуля), т.е. для
не равны нулю (они строго больше нуля), т.е. для 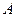 выполнены условия теоремы об LU-разложении и для нее единственно разложение вида:
выполнены условия теоремы об LU-разложении и для нее единственно разложение вида:
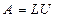 ,
,
где 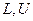 - нижняя с единицами на главной диагонали и верхняя треугольные матрицы соответственно, причем диагональные элементы матрицы
- нижняя с единицами на главной диагонали и верхняя треугольные матрицы соответственно, причем диагональные элементы матрицы 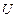
 .
.
Представим матрицу 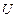 в следующем виде:
в следующем виде:
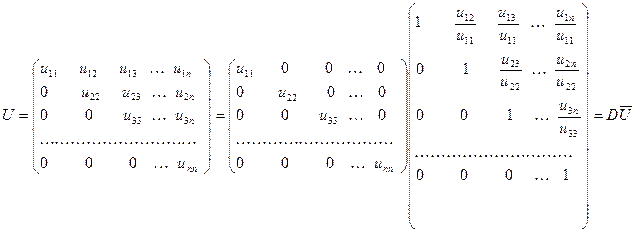 ,
,
тогда
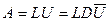 . (50)
. (50)
В силу симметричности матрицы 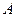 имеем:
имеем:
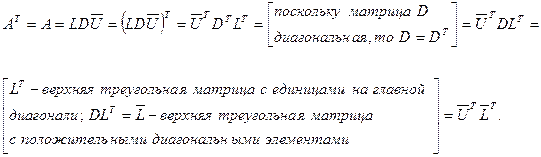
Итак, 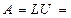
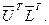 , где
, где  - нижние треугольные матрицы с единицами на главной диагонали,
- нижние треугольные матрицы с единицами на главной диагонали, 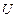 и
и 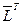 - верхние треугольные матрицы с положительными диагональными элементами. LU-разложение определяется однозначно, поэтому:
- верхние треугольные матрицы с положительными диагональными элементами. LU-разложение определяется однозначно, поэтому:
 ,
,
а разложение (50) будет иметь вид:
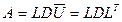 .
.
Поскольку элементы матрицы 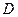 положительные, представим ее в виде:
положительные, представим ее в виде:
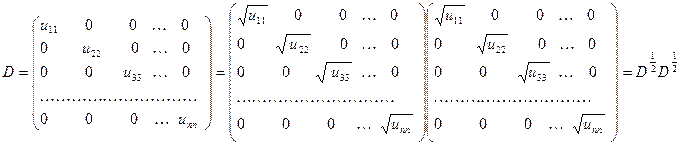
тогда
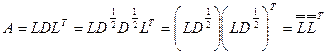 (50)
(50)
Разложение (50) называется разложением Холесского для симметричной положительно определенной матрицы.
Мы доказали
Теорему. Если 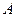 - симметричная положительно определенная
- симметричная положительно определенная 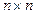 -матрица, то существует и единственно ее треугольное разложение
-матрица, то существует и единственно ее треугольное разложение 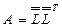 , называемое разложением Холесского, где
, называемое разложением Холесского, где 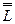 - нижняя треугольная матрица с положительными диагональными элементами.
- нижняя треугольная матрица с положительными диагональными элементами.
Построение симметричного разложения Холесского производится аналогично тому, как строится LU-разложение матрицы.
Метод Холесского для СЛАУ 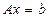 с симметричной и положительно определенной матрицей
с симметричной и положительно определенной матрицей 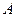 , основанный на разложении Холесского матрицы СЛАУ, выглядит следующим образом:
, основанный на разложении Холесского матрицы СЛАУ, выглядит следующим образом:
Шаг 1. Построить разложение Холесского матрицы СЛАУ: 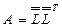 ;
;
Шаг 2. Решить СЛАУ 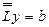 , в результате решения получить вектор
, в результате решения получить вектор 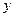 ;
;
Шаг 3. Решить СЛАУ 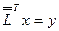 , в результате решения получить искомый вектор
, в результате решения получить искомый вектор 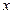 .
.
Пример. Пусть требуется решить СЛАУ
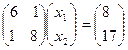 .
.
Матрица СЛАУ 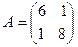 является симметричной, т.к.
является симметричной, т.к. 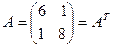 , и положительно определенной, поскольку
, и положительно определенной, поскольку 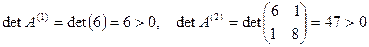 . Таким образом, для решения данной СЛАУ можно воспользоваться методом Холесского.
. Таким образом, для решения данной СЛАУ можно воспользоваться методом Холесского.
Шаг 1. Построим для матрицы 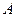 симметричное разложение:
симметричное разложение:
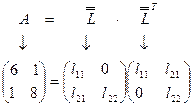 .
.
Элемент 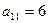 матрицы
матрицы 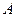 равен произведению первой строки матрицы
равен произведению первой строки матрицы 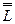 на первый столбец матрицы
на первый столбец матрицы 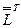 , т.е.
, т.е. 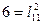 , откуда
, откуда 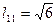 . Элемент
. Элемент 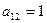 матрицы
матрицы 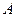 равен произведению первой строки матрицы
равен произведению первой строки матрицы 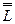 на второй столбец матрицы
на второй столбец матрицы 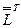 , т.е.
, т.е. 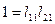 , откуда
, откуда 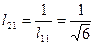 . Элемент
. Элемент 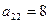 матрицы
матрицы 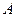 равен произведению второй строки матрицы
равен произведению второй строки матрицы 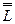 на второй столбец матрицы
на второй столбец матрицы 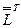 , т.е.
, т.е. 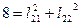 , откуда
, откуда 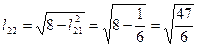 . Таким образом:
. Таким образом:
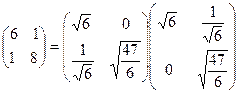 .
.
Шаг 2. Решаем СЛАУ 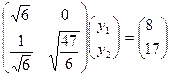 методом подстановки сверху вниз:
методом подстановки сверху вниз:
 ;
;
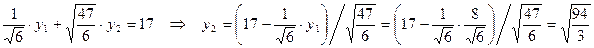 .
.
Шаг 3. Решаем СЛАУ 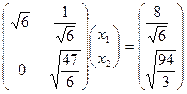 методом подстановки снизу вверх:
методом подстановки снизу вверх:
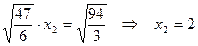 ,
,
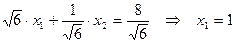 .
.
Вопросы
- Какая СЛАУ называется неоднородной?
- Теорема об LU-разложении матрицы.
- Для любой ли матрицы существует LU-разложение?
- Сколько различных LU-разложений существует для матрицы?
- Метод решения СЛАУ, основанный на LU-разложении матрицы системы.
- Для каких матриц существует симметричное разложение?
- Какая матрица называется полложительно определенной?
- Существует ли для положительно определенной матрицы LU-разложение?
- Метод Холесского.