Натуральная мощность и волновое сопротивление передачи. Распределение напряжения вдоль ЛЭП. Реактивная мощность.

Волновое сопротивление, определяющее токи прямой и обратной волн по соответствующим напряжениям, явля­ется функцией параметров линии электропередачи, связан­ных с ее конструкцией: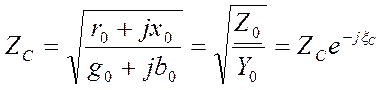

Волновое сопротивление колеблется от 400 Ом для ВЛ с одним проводом в фазе до 270 Ом при расщеплении про­водов в фазе на четыре. Аргумент волнового сопротивления ξ обычно отрицателен, так как r₀/х₀> g₀/b₀, а значение его лежит в пределах 1-2°. Коэффициент распростране­ния волны

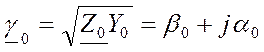
Для ВЛ величина β ₀= (3÷ 5)*10^-5 1/км, причем мень­шее значение относится к линиям с одним проводом в фа­зе, а большее — к линиям, выполненным расщепленными проводами. Значение α ₀ составляет 0, 06—0, 065 град/км.

Распределение напряжения вдоль длины линии опреде­ляется значением передаваемой мощности. Натуральная мощность течет по линии, когда сопротивление нагрузки на ее конце равно волновому сопротивлению Z_н=Z_с.

Натуральная мощность линии с номинальным напряже­нием равна

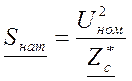
Для линий без потерь (r₀ = 0, g₀= 0) натуральная мощность является активной и определяется следующим выра­жением:

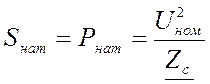
При этом для некоторой точки, расположенной на расстоянии х от конца передачи, векторы напряжения и тока, представлен­ные через прямые и обратные волны, могут быть найдены следующим образом:

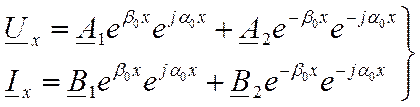
где A₁, А₂, B₁, В₂— комплексные постоянные интегрирова­ния; β ₀-коэффициент затухания (или постоянная зату­хания), который характеризует затухание (на единицу дли­ны) волны напряжения (тока) при ее распространении вдоль линии; α ₀ — коэффициент изменения фазы, характе­ризующий поворот вектора напряжения (тока) на единицу длины при распространении волны вдоль линии.

Преобразуя эти уравнения, получим основные соот­ношения, связывающие напряжения U₁, U₂и токи I₁, I₂ по концам протяженной линии с ее параметрами Z_c, α ₀, β ₀, l.

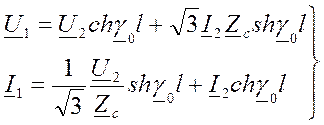
где ch, sh — гиперболические косинус и синус; Z_c — волно­вое сопротивление линии; Ом; γ ₀=β ₀+jα ₀— коэффициенту распространения волны на единицу длины, 1/км; l — длина линии электропередачи, км; 1, 2— индексы у векторов на­пряжения (тока) для начала и конца линии соответственно.

Рассмотрим соотношения между напряжениями и мощностями в конце и начале линии. Предположив линию без потерь, получим следующие, более простые выражения:

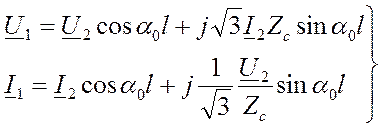
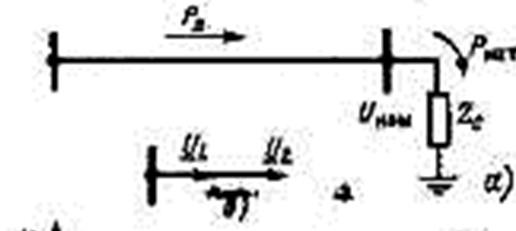
Рис. Распределение напряжения вдоль линии: а – передача натуральной мощности, б - холостой ход линии

Будем считать, что в конце линии на шины с напряжением U 2 включена нагрузка с сопротивлением Z ₂=r₂+jx₂ и мощностью 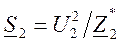. Предположим, что вектор напряжения в конце линии совпадает с осью действительных величин т.е. U ₂ =U₂. При принятых условиях первое из уравнений примет вид:

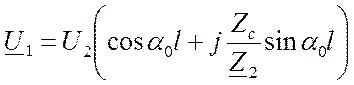(1)

При передаче по линии без потерь натуральной мощно­сти, т.е. при условии Z₂=Z_c, это уравнение упрощается следующим образом:

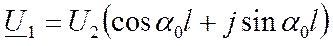(2)

из этого выражения и выражения для мощности следует:

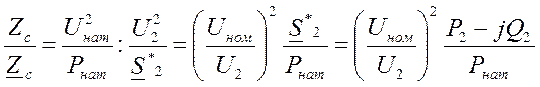(3)

Если принять U ₂= U_ном и подставить (3) в (1), то можно получить следующее выражение для напряжения 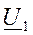, отстоящего на расстоянии l, км, от конца линии:

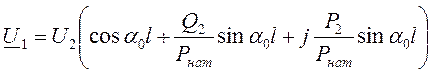(4)

С помощью него можно построить диаграммы распре­деления напряжения U _l вдоль длины линии при разных со­отношениях Q_л , Р_л и P_нат. При изменении длины линии от нуля l =0 до длины волны l =λ α l изменяется от 0 до 2π. Тогда, как это следует из (4), при изменении от l=0 до 1= λ конец вектора напряжения U ₁ описывает ок­ружность.

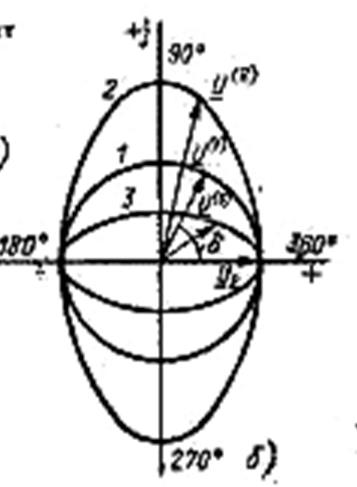На рис. б показаны диаграммы распределения на­пряжения U₁ вдоль линии длиной до 6000 км при Q ₂ =0. Зависимость 1 соответствует передаче мощности Р_л, равной натуральной, 2 —больше и 3 — меньше натуральной. Через U ⁽¹⁾, U ⁽²⁾, U⁽³⁾ обозначены напряжения в точке, рас­положенной на расстоянии 1000 км от конца линии соот­ветственно приР_л = Р_нат, Р_л = Р_нат и Р_я< Р_нат - угол сдвига между напряжениями U₂ и U⁽¹⁾ при передче по линии натуральной мощности обозначен δ.

Из (2) или (4) при Q_л= 0 следует, что при Р_л = Р _натзависимость 1 на рис. б — это окружность. При передаче по линии активной мощности больше натуральной с увеличением длины линии будет быстрее, чем в предыдущем случае, расти величина (Р₂/Р_нат)sinα ₀l. При этом окружность 1, образованная концом вектора U_l, будет вы тягиваться по вертикали, превращаясь в эллипс 2 на рис. б, меньшая ось которого равна U₂. Если по линии будет передаваться мощность меньше натуральной, то указанная окружность будет сжиматься вдоль той же оси, образуя эллипс 3, большая ось которого равна U₂. Предельный сличай режимов при Р_k< Р_нат - это холостой ход линии, когда Р_л = 0. При этом эллипс вырождается в прямую линию.

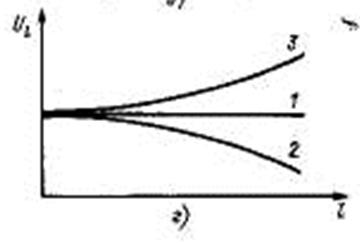
При неизменом модуле напряжения в начале линии U₁=const можно получить зависимости U₂ от длины линии. При P_l=P_нат это прямая l; при Р₂> Р_нaт — кривая 2, для которой U₁> U _L, т.е. напряжение в начале линии больше, чем в конце; при Р₂< P_нат кривая 3, для которой U₁< U _L, т.е. напряжение в начале линии меньше, чем в конце.

6-11Особенности режимов линий длиной в 1/2 и 1/4 волны.

Зависимость наибольшей передаваемой мощности Р_нб от длины линиив простейшем случае (линия без потерь) определяется следующим выражением: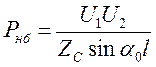

где U₁ U₂ - модули напряжений в начале иконце линии; Z_c —волновое сопротивление; α ₀l—волновая длина линии.

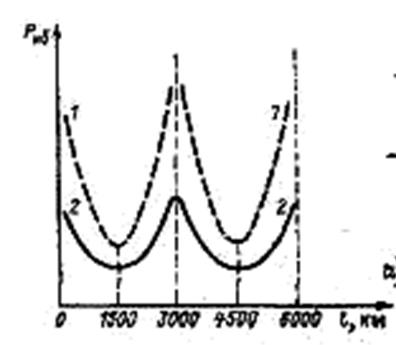
Рис.1. Зависимость наибольшей передаваемой мощности от длины линии: а – для линии без потерь (1) и с потерями (2),

Длина волны λ =6000 км.Если длина линии равна длине волны, то волновая длина линии λ _в = α ₀ l = 2π. В этом случае в линии без потерь Р_Нб = ∞, так как sin α ₀l = 0. При λ = 3000 км α ₀l = π и соответствен­но Р_Нб = ∞. При l = 1500 км и l =4500 км λ _в= π /2 и λ _в = 3/2 π. При этих длинах линии sin α ₀ = 1 и Р_Нб определяется на­пряжениями и волновым сопротивлением.

С точки зрения передачи наибольшей мощности наибо­лее выгодными являются линии длиной 3000 и 6000 км. Физически при этих длинах имеют место резонансы, так как индуктивное и емкостное сопротивления линий равны и результирующее реактивное сопротивление равно нулю. При этом в линии без потерь теоретически можно передать бесконечную мощность. Кривые 1 на рис. 1, а соответст­вуют этому случаю, При l =1500 и 4500 км реактивное сопротивление в линии имеет наибольшее значение и соот­ветственно Р_н6имеет наименьшее значение по сравнению с другими значениями l. Учет r_л, g_л а также сопротивления генераторов и трансформаторов меняют картину, и по линии при l=3000 и 6000 км можно передавать наибольшую, но не бесконечную мощность (кривые 2 на рис. 1, а).

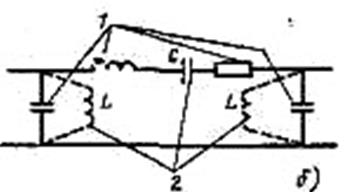Можно «настроить» линию искусственным включением емкости С и индуктивирсти L (рис. б) на определенную длину и создать условия для передачи наибольшей мощности. На рис: 1 — естественные параметры линии, 2— настраивающие параметры. Наиболее целесообразно для передачи наибольшей мощности настраивать линию на полуволну, т.е. изменять настраивающие параметры С и L так, чтобы в линии был резонанс. Техническая реализация и эксплуатация линий, настроенных на полуволну, связаны с большими трудностями.