Теоретические сведения. Для оценки эффектив­ности системы необходимо наблюдение за поведением ее модели под влиянием входных воздействий

Для оценки эффектив­ности системы необходимо наблюдение за поведением ее модели под влиянием входных воздействий, которые часто носят случайных характер. В результате такого наблюдения исследователь получает набор экспериментальных данных, на основе которых могут быть оценены характеристики системы. Такой вид моделирования называется имитационным.

При таком моделировании проводится статистический эксперимент, в основе которого лежит метод статистических испытаний - метод Монте-Карло.

Суть метода состоит в том, что результат испытания ставится в зависимость от значения некоторой случайной величины (СВ), распределенной по заданно­му закону. Поэтому результат каждого отдельного испытания также носит слу­чайный характер.

Проведя серию испытаний, получают множество частных значений наблюдаемой характеристики (выборку). Полученные статистические данные обрабатываются и представляются в виде численных оценок интересу­ющих исследователя величин (характеристик системы). Высокое качество статистических оценок возможно только при весьма большом числе испытаний.

Важно отметить, что метод статистических испытаний применим для ис­следования как стохастических, так и детерминированных систем.

Еще одной важной особенностью данного метода является то, что его ре­ализация практически невозможна без использования компьютера.

В качестве иллюстрации рассмотрим применение метода статистических испытаний для вычисления площади круга.

Необходимо найти площадь круга, радиус которого r=5 см и центр которого имеет координаты x = 1, y = 2.

Уравнение круга иммет вид

(x - 1)² + (y - 2)² = 25

Процедура оценки площади требует заключения круга в описанный около него квадрат, стороны которго равны диаметру круга и вершины которого определяютя непосредственно из геометрических свойств фигуры.

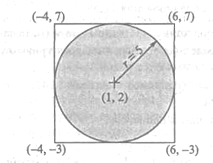
Оценка площади круга основана на предположении, что все точки квадрата равновероятны. Предположим, что выборка состоит из n точек квадрата и m из них попали внутрь круга или на окружность. Тогда площадь круга будет равна

,

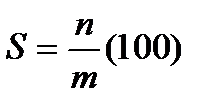где

100 – площадь круга (10х10).

На каждом шаге вычислений известны два случайных числа из интервала [0, 1], которые обозначим R₁ и R₂ . тогда координата точек квадрата x и y можно выразить через эти случайные числа

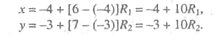
Пусть первая пара случайных чисел будет такой 0, 0589 и 0, 6733.

Вычислим координаты этой точки

х₁=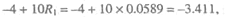

у₁=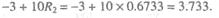

Эта точка попадет вовнутрь круга (или на его границы), если выполняется условие

(х₁-1)² + (у₁-2)² < =25

Так как 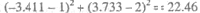меньше 25, то первая точка попала в площадь круга.

Аналогичным образом могут быть получены другие точки и определена площадь круга по вышеприведенной формуле.