Выталкивающая сила. Диффузия и внутреннее трение в жидкости

3.1 Выталкивающая сила. Закон Архимеда

Поскольку на разных уровнях жидкости давление будет разное – чем глубже, тем больше, возникает выталкивающая сила (Архимедова сила), действующая на тело, находящееся в жидкости или газе. Заменим тело, находящееся в жидкости, некоторым отвердевшим объёмом. Этот объём, помещённый в жидкость, будет находиться в состоянии равновесия, потому что его вес равен равнодействующей сил давления , действующих на его поверхность (рисунок 3.1). Отвердевший объём останется в равновесии при любом его ориентации в пространстве. Это состояние называется состоянием безразличного равновесия.

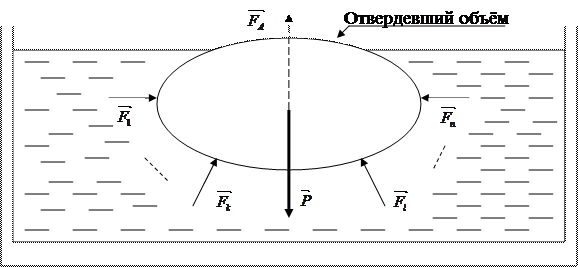Рисунок 3.1 – Силы, действующие на отвердевший объём, помещённый в жидкость

Соответственно, точка приложения выталкивающей силы совпадает с центром тяжести отвердевшего объёма. Центр тяжести тела совпадает с центром тяжести отвердевшего объёма только тогда, когда плотность тела во всех его точках одинакова. Иначе, эти два центра могут не совпадать.

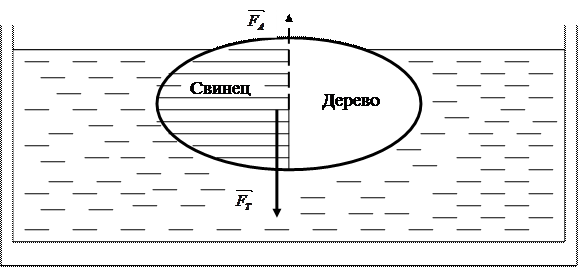Рисунок 3.2 – Силы, действующие на тело, помещённое в жидкость, если

Если взять сложенный из свинцовой и деревянной половинок шар, как показано на рисунке 3.2, то архимедова сила будет приложена к центру объёма шара. Свинцовая половинка тяжелее деревянной, поэтому сила тяжести 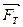будет смещена в сторону свинцовой половинки – к центру тяжести.

Если средняя плотность тела меньше плотности жидкости 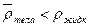, то в состоянии равновесия тело будет погружено в жидкость только частично. При этом точка приложения силы тяжести (к центру тяжести тела) не будет совпадать с точкой приложения архимедовой силы (к центру погруженного объёма). Как показано на рисунке 3.3, будет выполняться условие

,

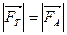т.е эти силы будут равны по модулю, а их векторы будут принадлежать одной прямой и будут противоположно направлены.

Рисунок 3.3 – Точки приложения 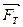и при условии .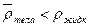

Иначе будет создан вращающий момент и равновесие тела будет нарушено.

3.2 Диффузия и внутреннее трение в жидкостях

Группа процессов, связанных с неоднородностями плотности, температуры или скорости упорядоченного перемещения отдельных слоёв вещества, носят название явления переноса.

К возникновению явлений переноса приводит «выравнивание» неоднородностей. К явлениям переноса относятся:

- диффузия;

- внутреннее трение;

- теплопроводность.

Диффузия – это явление взаимного проникновения тел друг в друга.

Количественно степень взаимного проникновения тел оценивается коэффициентом диффузии 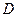. Для химически однородной жидкости коэффициент диффузии определяется с помощью выражения

. (3.1)

В выражении (3.1):

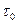- – средний период колебания одной молекулы жидкости около одного положения равновесия;

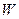- – энергия активации для перехода одной молекулы из одного устойчивого состояния в другое;

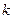- – постоянная Больцмана;

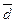- – среднее расстояние, на которое перемещается одна молекула жидкости из одного устойчивого состояния (положение равновесия) в другое;

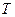- – температура жидкости.

Если температура жидкости достигает критического значения, то средняя скорость частиц в жидкости 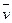будет стремиться к средней скорости молекул в реальном газе и коэффициент диффузии жидкости станет приблизительно равным аналогичному коэффициенту реального газа. Другими словами, тепловое движение жидкости приобретает характер теплового движения в газе.

Критической температурой 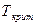жидкости называется температура, при которой полностью исчезают различия между свойствами жидкости и свойствами насыщенного пара.

Если в единице объёма двухкомпонентной жидкостной смеси содержится 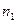молекул одного вида и 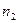молекул другого вида, тогда полное число молекул смеси будет равно 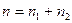. Пусть 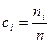– относительная концентрация молекул 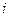-го вида, 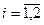. Предположим, что слой двухкомпонентной смеси жидкости движется в направлении 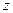, тогда:

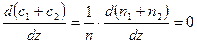, (3.2)

где 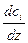– скорость изменения 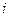-й концентрации по направлению .

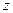Следовательно, выполняются два условия: и . Поэтому никаких гидродинамических потоков не возникает, но есть тепловое движение молекул, которое «выравнивает» концентрации, перенося массы каждой компоненты жидкости в направлении убывания её концентрации:

.

Этот процесс носит название диффузия (рисунок 3.4).

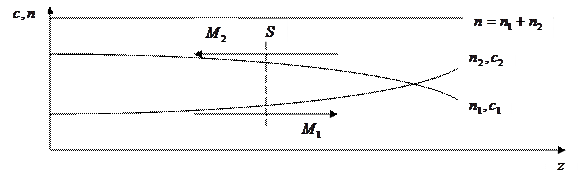Рисунок 3.4 – Перенос массы компоненты жидкости в направлении убывания её концентрации

Поток молекул 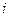-го вида 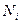через поверхность 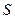, перпендикулярной оси 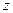, определяется выражением

. (3.3)

Знак «минус» показывает, что поток молекул направлен в сторону уменьшения концентрации .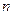

Обозначим 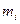массу молекулы жидкости 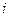-го вида. Тогда поток массы 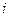-й компоненты жидкости равен:

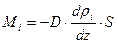, (3.4)

где 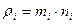– парциальная плотность 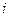-й компоненты жидкости, называемая абсолютной концентрацией.

Выражения вида (3.3) и (3.4) носят название закон Фика.

Сила трения между двумя слоями жидкости вычисляется по формуле

. (3.5)

В выражении (3.5):

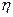- – коэффициент вязкости жидкости. Единица измерения – ;

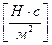- – производная скорости жидкости по направлению ;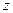

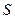- – площадь поверхности жидкости, по которой осуществляется трение.

Согласно второму закону Ньютона взаимодействие двух слоёв жидкости с силой 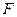– это процесс, в ходе которого от одного слоя к другому в единицу времени 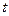передаётся импульс 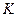, по величине равный 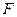. Тогда:

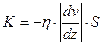. (3.6)

Знак «минус» обусловлен протеканию импульса 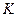в направлении уменьшения скорости .

Поскольку поток – это любое количество величины (энергии, импульса, частиц, массы), проходящее через поверхность площадью 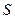в единицу времени 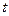, то с помощью выражения (3.6) рассчитывается величина потока импульса.

Если в жидкости вдоль оси 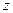создать скорость изменения температуры, то возникает поток тепла

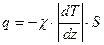, (3.7)

В выражении (3.7):

- – коэффициент теплопроводности, зависящий от свойств жидкости;

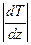- – скорость изменения температуры вдоль оси ;

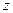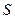- – поток тепла через поверхность , где .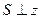

Единицы измерения потока тепла – 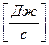или Ватт 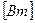. Единица измерения коэффициента теплопроводности – .

Выражение (3.7) носит название закона Фурье.