Процессы течения жидкости. Вязкость жидкости

6.1 Изменение давления в текущей жидкости

Известно, что давление в жидкости связано с величиной скорости течения. Поместим в жидкость изогнутую манометрическую трубку с обращённым навстречу потоку входным отверстием. Такая трубка называется трубка Пито (рисунок 6.1).

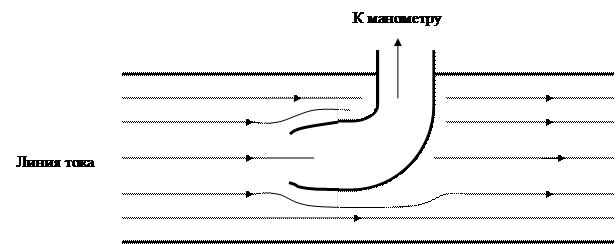Рисунок 6.1 – Трубка Пито

Рассмотрим линию тока, которая упирается своим концом в центр трубки Пито. Скорость жидкости изменяется от величины 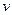(скорости потока далеко от отверстия трубки) до нуля (перед отверстием трубки). Поэтому, согласно уравнению Бернулли, давление, как перед отверстием трубки, так и внутри трубки Пито, будет больше, чем давление жидкости в точках, расположенных далеко от отверстия. Это связано с тем, что далеко от отверстия поток невозмущённый, а перед отверстием – возмущённый. Разница давлений будет равна величине 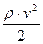. Это значит, что манометр, соединённый с трубкой Пито, покажет полное давление, равное

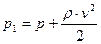. (6.1)

В выражении (6.1):

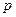- – давление невозмущённого потока, называемое статическим давлением;

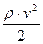- – давление возмущённого потока, называемое динамическим давлением.

Если в трубке Пито сделать боковое отверстие, тогда скорость и давление вблизи такого отверстия будут приблизительно равны скорости 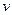и давлению 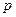невозмущённого потока вдали от отверстия трубки. Поэтому манометр, прикреплённый к такой трубке, называется зондом и показывает статическое давление жидкости (рисунок 6.2).

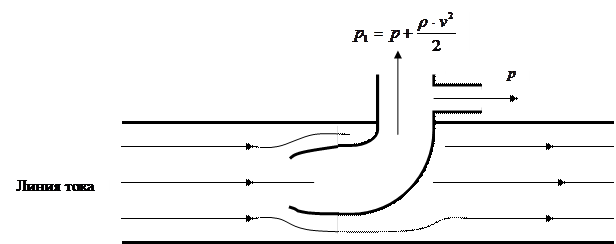Рисунок 6.2 – Зонд

По разности полного 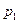и статического 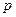давлений можно найти величину динамического давления 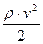, а следовательно и скорость течения жидкости 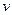, если плотность жидкости считается заранее известной. Если зонд и трубку Пито смонтировать вместе и подсоединить их к дифференциальному манометру, который измеряет разность давлений 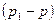, можно получить прибор для измерения скорости жидкости.

6.2 Силы внутреннего трения. Вязкость.

Всем жидкостям в большей или меньшей степени присуща вязкость или внутреннее трение.

Вязкость – это явление прекращения движения в жидкости после прекращения причин возникновения данного движения.

Погрузим в жидкость две параллельные друг другу пластины, длина которых превосходит расстояние между ними 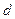(рисунок 6.3).

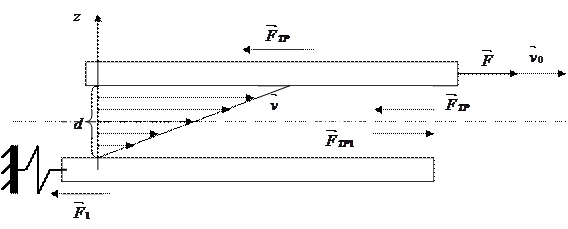Рисунок 6.3 – Движение двух параллельных друг другу пластин в жидкости

Одна пластинка начинает движение со скоростью 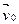под действием силы . Для сохранения постоянства скорости 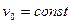необходимо действие силы трения 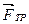в противоположном направлении и равной по величине, т.е. .

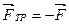Изменяя величины 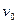, площадь пластин 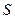и расстояние между ними 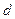, можно получить выражение:

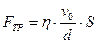. (6.2)

В выражении (6.2) величина 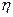зависит от вида и состояния жидкости (температуры и т.п.) и называется коэффициентом внутреннего трения, коэффициентом вязкости или просто вязкостью жидкости.

Вторая пластина при движении первой тоже придёт в движение в противоположном направлении под действием силы 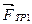, которая уравновешивается силой .

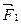Воздействие пластин друг на друга осуществляется через жидкость, заключённую между пластинами, передаваясь от одного слоя жидкости к другому. Исследования скорости частиц в разных слоях жидкости показывают, что процесс изменения скорости вдоль оси 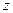носит следующий характер:

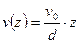. (6.3)

Частицы жидкости возле пластин приблизительно равны скоростям пластин, поэтому справедливо соотношение

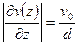. (6.4)

Подставляя (6.4) в (6.2) получаем

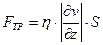. (6.5)

Из выражения (6.5) можно выразить коэффициент вязкости :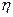

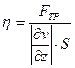. (6.6)

Определим единицы измерения вязкости:

.

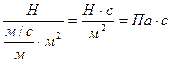Таким образом, единицей измерения вязкости является Паскаль на секунду [Па 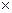с].

Коэффициент вязкости зависит и от температуры жидкости. При повышении температуры величина коэффициента вязкости уменьшается.

6.3 Ламинарное и турбулентное течения

Ламинарное течение – течение, при котором скользящие относительно друг друга слои жидкости, не перемешиваются.

Турбулентное течение – течение, в котором слои жидкости перемешиваются.

При турбулентном течении скорость частиц в каждой точке всё время изменяется. Таким образом, течение является нестационарным. Характер течения определяется безразмерной величиной – числом Рейнольдса:

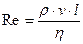. (6.7)

В выражении (6.7) величина 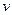– является средняя по сечению трубы скорость потока.

Вязкость жидкости 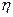является динамической вязкостью. С помощью соотношения вида 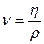определяется кинематическая вязкость. Посредством кинематической вязкости так же можно определить значение числа Рейнольдса:

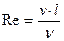. (6.8)

Число Рейнольдса может служить критерием подобия для течения жидкостей.

6.4 Течение жидкости в круглой трубе

При движении жидкости в круглой трубе:

- у стенок трубы скорость жидкости равна нулю ;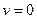

- на оси трубы скорость жидкости является максимальной .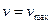

Рассмотрим процесс ламинарного течения жидкости в круглой трубе.

Для того, чтобы отследить динамику изменения скорости жидкости по продольному сечению трубы 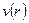, рассмотрим действие сил на внутренний воображаемый цилиндр, представляющий собой часть слоя жидкости:

1. Поскольку течение ламинарное, оно является стационарным. Поэтому скорость перемещения частиц жидкости постоянна. Векторная сумма внешних сил, приложенных к жидкости, равна нулю.

2. На основания внутреннего воображаемого цилиндра (рисунок 6.4)

Рисунок 6.4 – Течение слоя жидкости в круглой трубе

действуют силы давления, сумма которых составляет значение 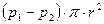. Такая сила действует в направлении течения жидкости.

3. На боковую поверхность воображаемого цилиндра действует сила трения, равная .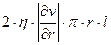

Условием стационарности в рассматриваемой ситуации является следующее условие:

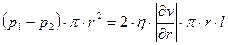. (6.9)

Поскольку при увеличении радиуса воображаемого цилиндра 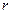скорость течения 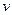уменьшается, то выполняется условие 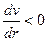. Тогда:

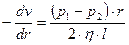. (6.10)

После разделения переменных проинтегрируем левую и правую части:

.

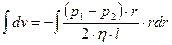После интегрирования получаем

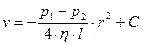. (6.11)

Константа 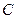выбирается исходя из того, что скорость жидкости на стенках трубы равна нулю. Это возможно при условии выполнения равенства 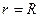, где 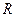является радиусом трубы. Поэтому

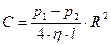. (6.12)

После подстановки (6.12) в (6.11) получаем

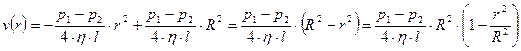.(6.13)

Исходя из этого скорость течения жидкости :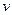

- на оси трубы

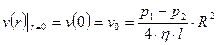; (6.14)

- у стенок трубы

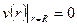. (6.15)

С учётом (6.14) запишем:

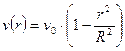. (6.16)

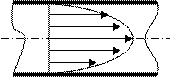Вывод: при ламинарном течении

скорость жидкости 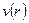изменяется с

расстоянием от оси трубы по параболи-

ческому закону, как показано на рисун-

ке 6.5. Рисунок 6.5 – Профиль скорос-

тей жидкости

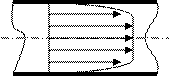Теперь рассмотрим процесс турбулентного течения жидкости в круглой трубе. Профиль средних скоростей при турбулентном течении изображён на рисунке 6.6.

Рисунок 6.6 – Профиль средних Из анализа рисунка следует:

скоростей при тур- – скорость жидкости в каждой точке из-

булентном течении меняется беспорядочно;

– средняя скорость остаётся примерно постоянной;

- возле стенок трубы скорость быстро уменьшается.

Предполагая, что течение ламинарное, вычислим поток жидкости 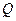– объём жидкости, проходящей через поперечное сечение трубы в единицу времени.

1. Сначала разобьём поперечное сечение трубы на кольца шириной 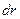, как показано на рисунке 6.7.

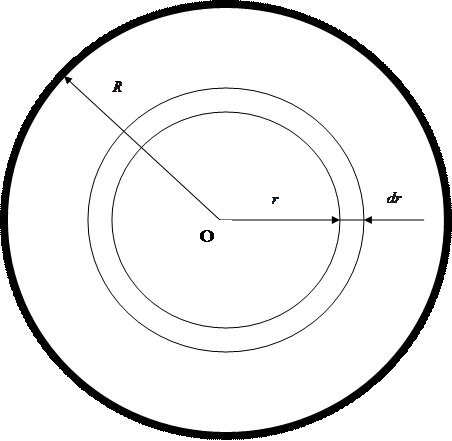
Рисунок 6.7 – Поперечное сечение трубы, условно разделённое на кольца

2. Через кольцо радиуса 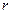за интервал времени 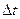пройдёт объём жидкости равный 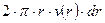, где 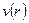– скорость течения в точке на расстоянии 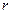от оси трубы.

С учётом (6.16) имеем:

.

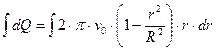После интегрирования левой и правой частей получаем:

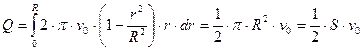, (6.17)

где 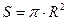– площадь поперечного сечения трубы.

Вывод: при ламинарном течении жидкости среднее по сечению трубы значение скорости течения равно половине значения скорости течения на оси трубы.

При подстановке (6.17) в (6.14) и домножении левой и правой части выражения на величину 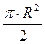получаем:

.

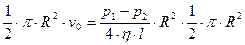После преобразования обеих частей в окончательном виде получаем

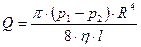. (6.18)

Выражение (6.18) носит название формула Пуазейля.

Вывод: поток жидкости при турбулентном течении:

а) прямо пропорционален:

- перепаду давления 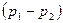на единицу длины трубы;

- радиусу трубы в четвёртой степени .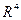

б) обратно пропорционален коэффициенту вязкости жидкости .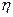

Соотношение (6.18) используется для определения вязкости жидкости.