Движение тела в жидкости. Электрические свойства жидкости

7.1 Движение тела в жидкости

При движении тела в жидкости на него действуют силы (рисунок 7.1). Обозначим равнодействующую этих сил .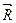

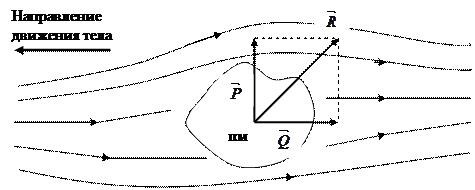Рисунок 7.1 – Действие сил на тело, движущееся в жидкости

Рассмотрим составляющие силы :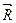

- сила 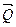, направленная в сторону, противоположную движению тела называется силой лобового сопротивления;

- сила , которая направлена перпендикулярно вектору силы 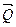– подъёмная сила.

Если тело имеет симметричную форму, то выполняется условие 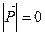. В идеальной жидкости, где вязкость отсутствует, равномерное движение тела должно происходить без лобового сопротивления, т.е. .

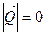Если жидкость реальная и обладает вязкостью, то тонкий слой жидкости прилипает к поверхности тела и движется вместе с ним, утаскивая за собой из-за трения последующие слои. По мере удаления от поверхности тела скорость слоёв становится меньше и, на определённом расстоянии от поверхности тела, оказывается практически невозмущённой движением тела.

Таким образом, тело оказывается окружённым слоем жидкости, где имеется градиент скорости. Данный слой является пограничным слоем. В нём действуют силы трения, которые оказываются приложенными к телу и приводят к возникновению лобового сопротивления.

При наличии пограничного слоя, как показано на рисунке 7.2, полное обтекание тела невозможно.

а) б)

Рисунок 7.2 – Обтекание тела а) в идеальной жидкости б) в реальной жидкости

Действия сил трения в поверхностном слое приводит к тому, что поток отрывается от поверхности тела, в результате чего позади тела возникают вихри (рисунок 7.2 «б»). Вихри относятся потоком и постепенно затухают за счёт силы трения. Энергия вихрей расходуется на нагревание жидкости. Давление в вихревой области оказывается пониженным, поэтому результирующая сил давления становится отличной от нуля, обуславливая лобовое сопротивление.

Таким образом, лобовое сопротивление 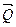складывается из сопротивления трению и сопротивления давлению. Сопротивление давлению сильно зависит от формы тела. Поэтому сопротивление давлению тождественно равно сопротивлению формы. Наименьшим сопротивлением давлению (формы) обладают тела хорошо обтекаемой каплевидной формы (рисунок 7.3).

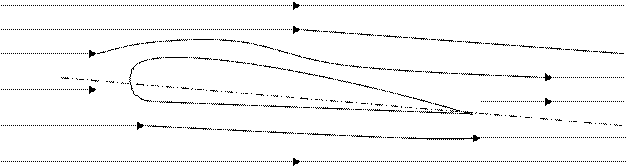Рисунок 7.3 – Обтекание тела каплевидной формы

Соотношение между сопротивлением трению и сопротивлением давлению определяется числом Рейнольдса (6.7). При этом:

- если число Рейнольдса 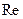мало, то основную роль играет сопротивление трению, а сопротивлением давлению можно пренебречь;

- при увеличении значения величины 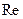роль сопротивления давлению начинает возрастать;

- если число 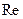велико, то основную роль играет сопротивление давлению. Сопротивление трению роли практически не играет.

7.2 Формула Стокса

Если число 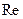мало, значит скорость движения тела относительно жидкости 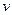и геометрические размеры тела 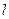малы. Сопротивление жидкости в этом случае обусловлено только силами трения. При этом модуль силы лобового сопротивления 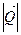прямо пропорционален вязкости жидкости 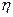, скорости набегающего потока 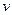и линейным размерам тела 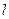. Поэтому сила сопротивления движению шарика в жидкости при малых скоростях равна

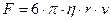. (7.1)

В выражении (7.1) величина 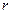есть радиус шарика, а само выражение является формулой Стокса.

Рассмотрим рисунок 7.4, где шарик в жидкости движется вертикально

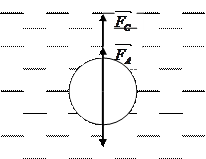вниз. На шарик, падающий вертикально

вниз (в жидкости), будут действовать три

силы:

1. Сила тяжести ;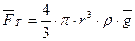

2. Архимедова сила ;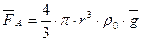

3. Сила Стокска .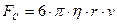

Рисунок 7.4 – Движение шарика Сила стокса зависит от скорости жидкости,

в жидкости вниз т.е. .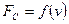

При достижении шариком определённой скорости 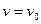, начнёт выполняться условие 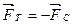. Поэтому шарик будет тонуть с постоянной скоростью, т.е. 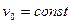. Значение скорости можно рассчитать 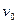из соотношения действующих на шарик сил, исходя из рисунка 7.4:

.

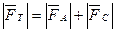Если в выражение подставить значения модулей сил, при условии, что 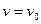, получим:

.

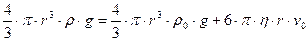Отсюда выражаем значение скорости :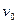

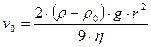. (7.2)

7.3 Подъёмная сила

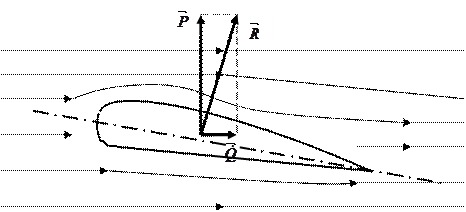Для возникновения подъёмной силы вязкость жидкости не имеет большого значения.

Рисунок 7.5 – Процесс возникновения подъёмной силы

Как следует из рисунка, линии тока сверху гуще, чем снизу, поэтому давление сверху будет меньше, чем снизу и поэтому из-за разности давлений возникает подъёмная сила .

Подъёмная сила возникает не только в идеальной жидкости, но и в жидкости, имеющей вязкость.