Уравнения движения жидкости в напряжениях

Получим общие уравнения движения жидкости, устанавливающие связь между внешними и внутренними силами, действующими на нее.

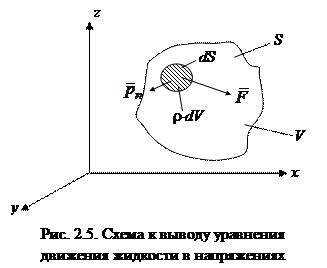Выделим в движущейся жидкости поверхностью S произвольный жидкий объем V (рис. 2.5), а внутри него – элементарную жидкую частицу с массой pdV и поверхностью dS. К этой частице приложены массовые силы с напряжением F и поверхностные силы с напряжением р_п. Запишем уравнение движения этой частицы, обозначая ускорение ее центра тяжести :

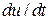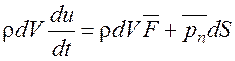. (2.24)

Просуммируем левую и правую части уравнения (2.24). Суммирование первых двух членов сводится к интегрированию по объему, а третьего члена – по площадкам, которыми элементарные частицы соприкасаются друг с другом. Согласно третьему закону Ньютона поверхностные силы по всем внутренним площадкам взаимно уничтожатся и останутся только поверхностные силы по площади S, ограничивающей объем V:

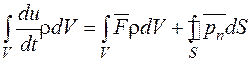z. (2.25)

Здесь и в дальнейшем кратные интегралы будут различаться только индексом, по которому производится суммирование. Преобразуем третий член уравнения (2.25), используя для этого зависимость (2.15),

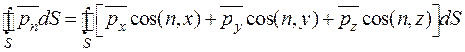. (2.26)

Применим к правой части этого равенства известное преобразование Гаусса-Остроградского, устанавливающее связь между объемным и поверхностным интегралами,

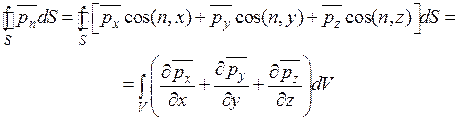. (2.27)

Подставляя правую часть (2.27) в уравнение (2.25), получим:

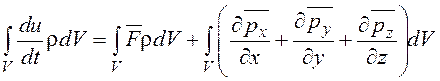. (2.28)

Все члены в уравнении (2.28) интегрируются по объему. Уравнения (2.25) и (2.28) являются уравнениями движения жидкого объема в интегральной форме. Их левая часть представляет главный вектор сил инерции, первый член правой части – главный вектор массовых сил, а второй – главный вектор поверхностных сил.

Получим дифференциальную форму уравнения движения, более удобную для изучения движения жидкости. Объединим все члены уравнения (2.28) под знаком интеграла, перенося силу инерции в правую часть,

.

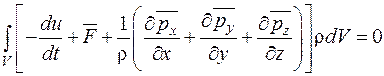Ввиду произвольности объема этот интеграл обращается в нуль только тогда, когда нулю тождественно равна подынтегральная функция:

.

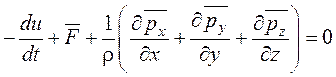В итоге получим дифференциальное уравнение движения жидкости в напряжениях:

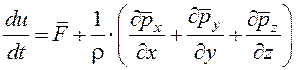, (2.29)

которое связывает ускорения с напряжениями массовых и поверхностных сил в данной точке потока и справедливо как для вязкой, так и невязкой жидкости.

Проектируя векторное уравнение (2.29) на оси координат, будем иметь:

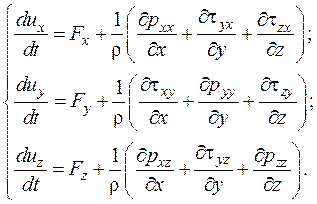(2.30)

Система уравнений (2.30) служит основой для разработки гидродинамики вязкой и невязкой жидкости.

2. СЛОВАРЬ ПОНЯТИЙ

Массовые силы – это силы, приложенные к каждой частице жидкости и пропорциональные ее массе.

Тензорной называется физическая величина, характеризуемая в данной точке вектором р, принимающим бесчисленное множество значений в зависимости от ориентации площадки.

Поверхностными называются силы, распределенные по поверхности S, ограничивающей выделенный объем жидкости.

3. МАТЕРИАЛЫ, ИСПОЛЬЗОВАННЫЕ В ПРОЦЕССЕ ОБУЧЕНИЯ

Возможен следующий план лекции:

1. Классификация сил, действующих в жидкости.

2. Свойства напряжений внутренних сил, действующих в жидкости.

3. Уравнения движения жидкости в напряжениях

4. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие силы называются массовыми? Приведите примеры.

2. Что Вы понимаете под напряжением поверхностных сил?

3. Чему равно напряжение силы тяжести?

4. Какие силы называются поверхностными? Приведите примеры.

5. Какими напряжениями характеризуются поверхностные силы?

6. Сформулируйте первое свойство напряжений поверхностных сил.

7. Сформулируйте второе свойство напряжений поверхностных сил.

8. Сформулируйте третье свойство напряжений поверхностных сил.

9. В каких случаях в жидкости не действуют касательные напряжения?

10. Что такое давление?

11. Выведите уравнение движения жидкости в напряжениях.

5. ЛИТЕРАТУРА

1. Альтшуль, А.Д. Гидравлика и аэродинамика / А.Д. Альтшуль, П.Г. Кисилев. – М.: Стройиздат, 1975. – 323 с.

2. Штеренлихт, Д.В. Гидравлика: учебник для вузов / Д.В. Штеренлихт. – М.: Энергоатомиздат, 1984. – 640 с.

3. Повх, И.Л. Техническая гидродинамика / И.Л. Повх. – Л.: Машиностроение, 1969. – 524 с.

4. Чугаев, Р.Р. Гидравлика / Р.Р. Чугаев. – Л.: Энергия, 1982. – 600 с.

5. Федяевский, К.К. Гидромеханика: учебник для вузов /
К.К. Федяевский, Я.И. Войткунский, Ю.И. Фаддеев. – Л.: Судостроение, 1968. – 568 с.

ГИДРОСТАТИКА ЖИДКОСТИ

1. ВВЕДЕНИЕ

Гидростатика – раздел гидромеханики, изучающий равновесие жидкости. Различают абсолютное равновесие жидкости, когда из массовых сил действует только сила тяжести, и относительное равновесие, когда на жидкость, кроме сил тяжести, действуют инерционные силы. В этом случае объем жидкости может двигаться не деформируясь, то есть как абсолютно твердое тело, в то время как движение частиц жидкости друг относительно друга отсутствует.

Здесь мы рассмотрим только гидростатику несжимаемой жидкости.

2. ОСНОВЫ НАУЧНО-ТЕОРЕТИЧЕСКИХ ЗНАНИЙ ПО МОДУЛЮ

2.1. Дифференциальное уравнение равновесия жидкости
(уравнение Эйлера)

Связь между массовыми силами и давлениями в жидкости, находящейся в равновесии, устанавливается уравнениями гидростатики для получения которых необходимо в уравнении движения жидкости в напряжениях прировнять к нулю производную скорости по времени.

В покоящейся жидкости касательные напряжения равны нулю и выполняется следующее условие:

;

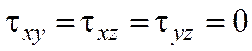Полагая 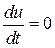и учитывая приведенное равенство, мы можем из дифференциального уравнения движения жидкости в напряжениях

;

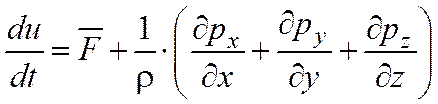записать уравнение гидростатики в следующем виде:

.

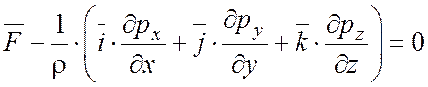Знак «–» появился при переходе от напряжений к давлению.

Используя понятие градиента скалярной функции это уравнение можно записать в виде соотношения:

,

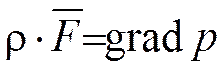представляющего собой уравнение равновесия жидкости в векторной форме. Полученное уравнение было выведено Эйлером и носит его имя. Оно справедливо как для абсолютного, так и для относительного равновесия жидкости.

2.2. Уравнения гидростатики и их интегрирование

Выявим условия интегрируемости уравнения Эйлера. Для этого применим к нему дифференциальную операцию rot, считая что ρ = const:

.

Как известно, вихрь потенциального вектора равен нулю, то есть

;

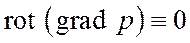тогда

,

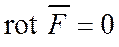а раз вихрь вектора равен нулю, значит он потенциален, то есть поле направлений массовых сил обладает потенциалом U:

.

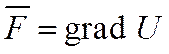Таким образом, равновесие несжимаемой жидкости возможно только в случае действия на неё потенциальных массовых сил.

Чтобы интегрировать уравнение равновесия, подставим в него

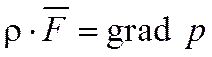
Значение 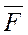, выражаем через потенциал U:

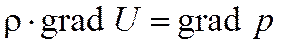
Или

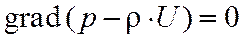. (3.1)

Операция вычисления градиента аналогична дифференцированию по координатам x, y, z. Согласно (3.1) выражение, находящееся под знаком градиента, постоянно и не зависит от координат x, y, z. На основании этого получим интеграл уравнения равновесия

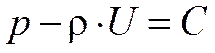, (3.2)

где постоянная С не зависит от координат, то есть одинакова для всех точек пространства. Определим эту постоянную, исходя из граничных условий.

Пусть при 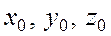известны значения U и p, то есть U = U₀, p = p₀, а значит:

.

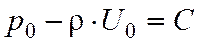Подставляя эти значения в найденный нами интеграл (3.2), получаем

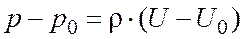. (3.3)

Отсюда:

.

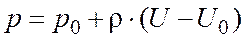Величина 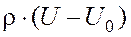представляет результат воздействия на жидкость только массовых сил и не зависит от давления p₀. В силу этого если в точках на границе жидкости увеличить давление p₀ на некоторую величину, не нарушая при этом равновесие жидкости, то в соответствии с (3.3) во всех точках объёма, занятого жидкостью, давление увеличится на эту же величину. Это составляет закон Паскаля, согласно которому приложенное к поверхности жидкости давление передаётся жидкостью по всем направлениям одинаково.

Рассмотрим важный частный случай, когда на покоящуюся жидкость действует лишь сила тяжести. Ранее нами было получено, что потенциал силы тяжести равен

.

Исходя из этого, выражение (3.3) можно записать в следующем виде

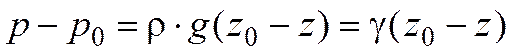
или

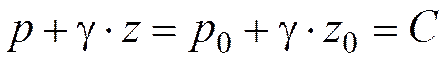. (3.4)