Классификация сил, действующих в жидкости

При изучении механики твердого тела обычно рассматривают две категории сил – сосредоточенные и распределенные. В жидкости, как правило, необходимо исследовать действие только распределенных сил, так как приложение к ней сосредоточенных сил обусловливает появление разрывов в жидкости.

Для классификации сил, действующих в жидкости, применим известный из курса сопротивления материалов метод сечений: выделим в движущейся жидкости произвольный жидкий объем V, ограниченный поверхностью S (рис. 2.1), и мысленно отбросим всю жидкость вне этого объема. При этом внутренние силы, действующие между выделенной и отброшенной частями жидкости, перейдут в категорию внешних сил, распределенных по поверхности S. Таким образом, влияние отброшенной жидкости проявляется в виде поверхностных сил, приложенных к поверхности раздела S.

Кроме них, в любой точке объема V действуют массовые силы, пропорциональные массе жидкости, заключенной в элементарном объеме ∆ V, окружающем данную точку (рис. 2.1). Рассмотрим более подробно эти две категории сил.

Массовыми называются силы, приложенные к каждой частице жидкости и пропорциональные ее массе. Обозначим через ∆ f массовую силу, приложенную к жидкой частице с массой ρ ∆ V, и введем понятие напряжения массовой силы, характеризуемого в данной точке вектором F, определяемым как предел отношения вектора массовой силы к массе частицы:

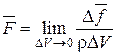. (2.1)

Если вектор F постоянный, то напряжение массовых сил равно отношению массовой силы, действующей на объем, к массе этого объема.

Напряжение массовых сил имеет размерность ускорения [F] = LT^-2.

Составляющие вектора F на оси декартовых координат обозначим F_x, F_y, F_z. В общем случае F является функцией радиуса-вектора точки r и времени t; F = F (r, t).

К массовым силам относятся, например, силы тяжести, силы инерции и электромагнитные силы.

Определим вектор напряжения массовых сил в наиболее важном частном случае действия силы тяжести. Вес элементарной частицы ∆ Р = ρ ∆ Vg. При выборе направления оси z вверх массовая сила 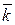, где
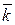= орт оси z.

Получаем что

F = –kg (2.2)

или

F_x = 0; F_y =0; F= – g. (2.3)

В ряде практически важных случаев массовые силы потенциальны. Обозначим через U потенциал напряжения массовых сил. При этом вектор их напряжения F можно определить как градиент скалярной функции U:

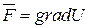(2.4)

или

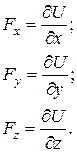(2.5)

В случае, когда массовой силой является сила тяжести, согласно (2.3) и (2.5):

,

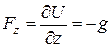откуда следует, что

U = – gz+C. (2.6)

Произвольную постоянную С можно отбросить, так как ее величина не влияет на определение вектора F.

Таким образом, потенциал силы тяжести определяется выражением:

U = –gz. (2.7).

Поверхностными называются силы, распределенные по поверхно­сти S, ограничивающей выделенный объем жидкости (рис. 2.2).

Обозначим через ∆ р_п поверхностную силу, приложенную к площадке ∆ S с внешней нормалью п. В общем случае ∆ р_n действует под углом к внешней нормали. Введем понятие вектора напряжения поверхностных сил в данной точке поверхности, определяя его как предел отношения:

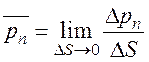. (2.8)

Из (2.8) следует, что вектор напряжения поверхностных сил представляет отношение поверхностной силы к величине элементарной площадки. Следовательно, р_п имеет размерность L^-1 MT^-2.

В общем случае р_п не является обычным вектором. Его величина в данной точке зависит от ориентации площадки, выделенной внутри объема жидкости. Иными словами, если через данную точку провести одинаковые по величине, но различные по ориентации площадки, то действующие на них векторы р_п напряжения поверхностных сил будут различны. Поэтому в общем случае р_п зависит от радиуса-вектора точки, ориентации площадки и времени:

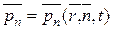. (2.9)

Физическая величина, характеризуемая в данной точке вектором р, принимающим бесчисленное множество значений в зависимости от ориентации площадки, называется тензорной.

Одной из важнейших задач гидромеханики является определение гидродинамических реакций, действующих со стороны жидкости на тело. Когда поверхность S в жидкости совпадает с поверхностью твердого тела, то это свидетельствует, что к ней со стороны жидкости приложены напряжения р_п. Следовательно, элементарная сила воздействия dR со стороны жидкости на площадку поверхности тела dS определится выражением:

dR = p_ndS,

а элементарный момент относительно начала координат:

,

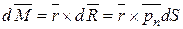где r – радиус-вектор центра площадки.

Интегрируя dR и dM по поверхности S тела, получим общие формулы для результирующей R и момента М гидродинамических сил, действующих на тело:

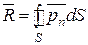; (2.10)

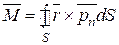. (2.11)

Для использования общих выражений (2.10) и (2.11) требуется отыскать зависимости напряжений р_п от скорости течения жидкости, формы тела и физических свойств жидкости. Исследование этих зависимостей и явится одной из главных задач курса.

Подчеркнем, что массовые силы, действующие в жидкости, влияют на гидродинамические реакции, возникающие на теле, лишь через напряжения поверхностных сил.