
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ISBN 978-985-418-900-0
|
|
ББК 30.123я73
Ó Липский В. К., Комаровский Д. П., 2009
Ó УО «Полоцкий государственный университет», 2009
МОДУЛЬ 0
ВВЕДЕНИЕ В КУРС «ТЕХНИЧЕСКАЯ ГИДРОМЕХАНИКА»
1. ПРЕДМЕТ ГИДРАВЛИКИ И ГИДРОМЕХАНИКИ
Теоретическая механика, изучая простейшие механические формы движения и взаимодействия материальных тел, отвлекается от многих их действительных свойств и использует в качестве допустимой абстракции понятия материальной точки и системы материальных точек.
Материальная система может быть как дискретной, состоящей из отдельных материальных точек, например, в задачах движения планет солнечной системы, так и сплошной, представляющей непрерывное распределение вещества и физических характеристик его состояния и движения в пространстве. В этом случае систему называют сплошной материальной средой или, короче, сплошной средой.
Примером сплошной среды является неизменяемая среда или абсолютно твердое тело. Более общий образ изменяемой сплошной среды объединяет в механике как упругие и пластичные, так и жидкие и газообразные тела.
Раздел теоретической механики, занимающийся движениями данного ряда изменяемых сфер, носит наименование механики сплошных сред, а часть ее, относящаяся к жидким и газообразным телам - механики жидкости и газа. Этот термин является синонимом термина «гидромеханика».
Механика жидкости (гидромеханика) развивалась за рубежом и в России, а затем и в СССР, по двум направлениям:
1) по направлению, свойственному техническим наукам (изучаемым в технических учебных заведениях);
2) по математическому направлению (с использованием обширного и относительно сложного математического аппарата, изучаемого главным образом на механико-математических факультетах).
В связи с этим создалось положение, когда в области единой науки механики жидкости стали различать две разные науки (два разных метода исследования): «техническую механику жидкости» («техническую гидромеханику»), называемую часто «гидравликой и «математическую механику жидкости» («математическую гидромеханику»).
Различие между этими науками, имеющими один и тот же объект исследования, заключается в следующем.
В технической механике жидкости (гидравлике) при решении различных практических задач широко используются те или иные допущения и предположения, упрощающие рассматриваемый вопрос. Достаточно часто гидравлические решения основываются на результатах экспериментов, и потому в технической механике жидкости приводят относительно много различных эмпирических и полуэмпирических формул. При этом стремятся к оценке только главных характеристик изучаемого явления и часто оперируют теми или иными интегральными и осредненными величинами, которые дают достаточную для технических приложений характеристику рассматриваемых явлений. Например, в технической механике жидкости часто пользуются понятием средней скорости движения жидкости в том или другом поперечном сечении потока. По своему характеру техническая механика близка к известным дисциплинам – строительной механике и сопротивлению материалов, в которых под тем же углом зрения изучаются вопросы механики твердого тела. Следует учитывать, что гидравлика, являясь общетехнической дисциплиной, должна рассматриваться как «профессиональная физика жидкого тела», в которой, в частности, даются основы соответствующих гидромеханических расчетов, используемых при проектировании инженерных сооружений, конструкций, а также надлежащих технологических процессов.
В математической механике жидкости, как было отмечено, широко используется относительно сложный математический аппарат, не изучаемый в технических вузах. Этот аппарат прилагается также к несколько упрощенным схемам движения жидкости. Однако в этом методе исследования мы все же не прибегаем к различного рода допущениям и не оперируем различными осредненными величинами в такой мере, как в технической механике жидкости. Решения, получаемые в математической гидромеханике, оказываются более строгими в математическом отношении. По своему характеру математическая механика жидкости сходна с математической теорией упругости (рассматривающей вопросы механики твердого тела), изучаемой в университетах.
Как показал опыт, методы математической механики жидкости часто оказываются столь сложными, что большинство практических задач невозможно решить, следуя этим методам. Этим и объясняется возникновение и развитие технической, прикладной науки – технической механики жидкости, то есть гидравлики, которая стремится дать приближенные ответы на все те вопросы, связанные с движущейся или покоящейся жидкостью, которые ставит перед нами практика.
Можно сказать, что в технической гидромеханике (в гидравлике) приближенно решаются сложные задачи при помощи простых методов. В математической же гидромеханике относительно точно решаются только некоторые простейшие задачи при помощи сложных методов. Следует отметить, что в последнее время мы все чаще сталкиваемся с вопросами, которые приходится решать, сочетая методы технической и математической гидромеханики, причем иногда бывает трудно провести границу между ними.
Необходимо отметить, что техническая механика жидкости (гидравлика), представляющая собой обширную, самостоятельную, сложившуюся техническую науку, включает в себя много различных разделов, касающихся отдельных сторон рассматриваемой проблемы. Разумеется, эти разделы должны излагаться в курсах «Технической механики жидкости» для разных технических специальностей.
Из сказанного выше видно, что термины «гидравлика», «техническая гидромеханика» и «техническая механика жидкости» следует рассматривать как термины, имеющие одинаковое значение (как бы синонимы). Необходимо учитывать, что само слово «гидравлика» произошло от слияния двух греческих слов, из которых первое значит «вода», а второе – «труба», «канал», «струя». Как видно, ранее считали, что гидравлика занимается изучением движения или покоя только воды. Однако в настоящее время термин «гидравлика» (а также «гидромеханика») рассматривается в более широком смысле: объектом изучения в гидравлике является любая жидкость, а не только вода.
Мы в дальнейшем будем, в основном, пользоваться терминами гидравлика, хотя будем рассматривать целый ряд результатов, полученных в гидромеханике.
Гидравлика (техническая гидромеханика) делится на две части: гидростатику и гидродинамику. В гидростатике рассматриваются механические свойства жидкостей, законы равновесия жидкостей и действие их на соприкасающиеся с ними твердые тела.
В гидродинамике изучаются законы движения жидкостей и взаимодействия их с соприкасающимися твердыми телами.
2. КРАТКИЙ ИСТОРИЧЕСКИЙ ОБЗОР
РАЗВИТИЯ МЕХАНИКИ ЖИДКОСТИ
Первым научным трудом в области гидравлики считается трактат Архимеда (287 – 212 гг. до н.э.) «О плавающих телах», хотя некоторые законы гидравлики были, видимо, известны и ранее, так как задолго до Архимеда строились оросительные каналы и водопроводы.
В древнем Египте, Индии, Китае были построены каналы и водохранилища грандиозных по тем временам размеров. Так, глубина некоторых водохранилищ в Индии достигала 15 м, в Китае около 2500 лет назад был построен Великий канал длиной около 1800 км, который соединял приустьевые участки крупных рек страны. В Риме 2300 лет назад был построен первый водопровод.
На территории бывшего советского Союза также были построены многочисленные каналы и сооружения для добычи и транспортирования воды. Земледелие в районах Кавказа и Средней Азии велось с применением орошения. Некоторые из каналов, построенных в низовьях Амударьи около 2000 лет назад, используются и по сей день (естественно, после многоразовых ремонтов и реконструкций).
Старинные летописи и другие источники содержат много сведений о строительстве в России различных сооружений на реках, о развитии водных путей, о попытках создания механизмов, использующих энергию водного потока, и о многих других конструкциях, осуществление которых было бы невозможно без знания основ гидравлики. Так, еще в X – XI вв. на Руси существовали водопроводы из гончарных и деревянных труб, в 1115 г. был построен наплавной мост через Днепр у Киева. В XIV – XV вв. применялась добыча воды из подземных источников, оборудованных довольно совершенными водопроводными устройствами.
В средние века в России возводились многочисленные плотины на реках. Так, в 1516 г. была построена плотина из камня на р. Неглинке в Москве.
 Подъем в развитии гидравлики начался только через 17 веков после Архимеда. В XV – XVI вв. Леонардо да Винчи (1452 – 1519) написал работу «О движении и измерении воды», которая была опубликована лишь через 400 с лишним лет после ее создания. С. Стевин (1548 – 1620) написал книгу «Начала гидростатики», Галилео Галилей (1564 – 1642) в 1612 г. в трактате «Рассуждение о телах, пребывающих в воде, и о тех, которые в ней движутся» рассмотрел основные законы плавания и гидростатический парадокс, Е. Торричелли (1608 – 1647) получил формулу скорости истечения невязкой жидкости из резервуаров через отверстия, Б. Паскаль (1623 – 1662) открыл закон о передаче давления в жидкости, прямым следствием чего явилось появление в средние века большого количества простых гидравлических машин (гидравлические прессы, домкраты и т.п.), И. Ньютон (1643 – 1727) в 1686 г. сформулировал гипотезу о внутреннем трении в жидкости.
Подъем в развитии гидравлики начался только через 17 веков после Архимеда. В XV – XVI вв. Леонардо да Винчи (1452 – 1519) написал работу «О движении и измерении воды», которая была опубликована лишь через 400 с лишним лет после ее создания. С. Стевин (1548 – 1620) написал книгу «Начала гидростатики», Галилео Галилей (1564 – 1642) в 1612 г. в трактате «Рассуждение о телах, пребывающих в воде, и о тех, которые в ней движутся» рассмотрел основные законы плавания и гидростатический парадокс, Е. Торричелли (1608 – 1647) получил формулу скорости истечения невязкой жидкости из резервуаров через отверстия, Б. Паскаль (1623 – 1662) открыл закон о передаче давления в жидкости, прямым следствием чего явилось появление в средние века большого количества простых гидравлических машин (гидравлические прессы, домкраты и т.п.), И. Ньютон (1643 – 1727) в 1686 г. сформулировал гипотезу о внутреннем трении в жидкости.
 Однако перечисленные разработки и открытия касались только отдельных разделов гидравлики. Формирование гидравлики как науки на прочной теоретической основе стало возможным только после работ академиков Петербургской Академии наук М.В. Ломоносова (1711 – 1765), Д. Бернулли (1700 – 1782) и Э. Эйлера (1707 – 1783).
Однако перечисленные разработки и открытия касались только отдельных разделов гидравлики. Формирование гидравлики как науки на прочной теоретической основе стало возможным только после работ академиков Петербургской Академии наук М.В. Ломоносова (1711 – 1765), Д. Бернулли (1700 – 1782) и Э. Эйлера (1707 – 1783).
М.В. Ломоносов в 1760 г. в диссертации «Рассуждение о твердости и жидкости тел» сформулировал законы сохранения вещества и энергии.
 Д. Бернулли (1700 – 1782) – выдающийся физик и математик – родился в Гронингене (Голландия). С 1725 по 1733 г. жил в Петербурге, являлся профессором и членом Петербургской Академии наук. В Петербурге он написал свой знаменитый труд «Гидродинамика», который был впоследствии опубликован (в 1738 г.) в г. Страсбурге. В этом труде он осветил ряд основополагающих гидравлических вопросов и в частности объяснил физический смысл слагаемых, входящих в современное уравнение установившегося движения (идеальной жидкости), носящее его имя.
Д. Бернулли (1700 – 1782) – выдающийся физик и математик – родился в Гронингене (Голландия). С 1725 по 1733 г. жил в Петербурге, являлся профессором и членом Петербургской Академии наук. В Петербурге он написал свой знаменитый труд «Гидродинамика», который был впоследствии опубликован (в 1738 г.) в г. Страсбурге. В этом труде он осветил ряд основополагающих гидравлических вопросов и в частности объяснил физический смысл слагаемых, входящих в современное уравнение установившегося движения (идеальной жидкости), носящее его имя.
Д. Бернулли в 1738 г. опубликовал выведенное им важнейшее уравнение, названное его именем. Это уравнение служит основой теоретических построений и практических расчетов в области гидравлики.
 Л. Эйлер (1707 – 1783) – великий математик, механик и физик – родился в г. Базеле (Швейцария). Жил в Петербурге с 1727 до 1741 г. и с 1766 г. до конца жизни. Был членом Петербургской Академии наук. Эйлер не только подытожил и обобщил в безупречной математической форме работы предшествующих авторов, но составил известные дифференциальные уравнения движения и относительного равновесия жидкости, носящие его имя, а также опубликовал целый ряд оригинальных решений гидравлических задач, широко используя созданный к тому времени математический аппарат.
Л. Эйлер (1707 – 1783) – великий математик, механик и физик – родился в г. Базеле (Швейцария). Жил в Петербурге с 1727 до 1741 г. и с 1766 г. до конца жизни. Был членом Петербургской Академии наук. Эйлер не только подытожил и обобщил в безупречной математической форме работы предшествующих авторов, но составил известные дифференциальные уравнения движения и относительного равновесия жидкости, носящие его имя, а также опубликовал целый ряд оригинальных решений гидравлических задач, широко используя созданный к тому времени математический аппарат.
Л. Эйлер в 1755 г. вывел системы дифференциальных уравнений равновесия и движения жидкости.
Интересно, что наряду с гениальными теоретическими работами М.В. Ломоносова, Д. Бернулли и Л. Эйлера известны их исследования в области создания гидравлических приборов и устройств. М.В. Ломоносов изобрел универсальный барометр, вискозиметр (прибор для исследования вязкости жидкости), прибор для определения скорости течений в море. М.В. Ломоносов занимался также усовершенствованием гидравлических машин и устройств. Д. Бернулли изобрел водоподъемник, установленный в селе Архангельском под Москвой, и поднимавший воду на высоту 30 м. Л. Эйлер предложил конструкцию турбины, вывел так называемое «турбинное уравнение», создал основополагающие труды в теории корабля.
В 1791 г. в Петербурге А. Колмаков издал книгу «Карманная книжка для вычисления количества воды, протекающей через трубы, отверстия», которая явилась первым справочником по гидравлике.
Первое в России учебное пособие по гидравлике было выпущено в 1836 г. П.П. Мельниковым под названием «Основания практической гидравлики или о движении воды в различных случаях».
 Перечисленные теоретические работы положили начало бурному развитию гидравлики. Велики заслуги ученых Д. Полени (1685 – 1761), который работал в области истечения через отверстия и водосливы; А. Шези (1718 – 1798), изучавшего равномерное движение жидкости; П. Дюбуа (1734 – 1809), занимавшегося движением наносов в реках, сопротивлениями движению воды в руслах; Д. Вентури (1746 – 1822), исследовавшего истечение через отверстия и насадки; Ю. Вейсбаха (1806 – 1871), в основном известного работами в области сопротивлений движению жидкости; А. Базена (1829 – 1897), изучавшего равномерное движение и истечение жидкости через водосливы; О. Рейнольдса (1842 – 1912), внесшего большой вклад
Перечисленные теоретические работы положили начало бурному развитию гидравлики. Велики заслуги ученых Д. Полени (1685 – 1761), который работал в области истечения через отверстия и водосливы; А. Шези (1718 – 1798), изучавшего равномерное движение жидкости; П. Дюбуа (1734 – 1809), занимавшегося движением наносов в реках, сопротивлениями движению воды в руслах; Д. Вентури (1746 – 1822), исследовавшего истечение через отверстия и насадки; Ю. Вейсбаха (1806 – 1871), в основном известного работами в области сопротивлений движению жидкости; А. Базена (1829 – 1897), изучавшего равномерное движение и истечение жидкости через водосливы; О. Рейнольдса (1842 – 1912), внесшего большой вклад
в изучение ламинарного и турбулентного режимов
движения.
Во второй половине XIX века в России появляются работы, оказавшие большое влияние на последующее развитие гидравлики. И.С. Громека (1851 – 1889) создал основы теории винтовых потоков и потоков с поперечной циркуляцией. Д.И. Менделеев (1834 – 1907) в своей работе «О сопротивлении жидкости и воздухоплавании» в 1880 г. привел важные выводы о наличии двух режимов движения жидкости (ламинарного и турбулентного). Далее Н.П. Петров (1836 – 1920) сформулировал закон внутреннего трения в жидкости. Н.Е. Жуковский (1847 – 1921) создал теорию гидравлического удара в водопроводных трубах, теорию движения наносов в реках и разработал основополагающие предложения в области фильтрации.
 Труды академика Н.Н. Павловского (1884 – 1937) в области равномерного и неравномерного движения, фильтрации через земляные плотины и под гидротехническими сооружениями явились большим вкладом в развитие гидравлики и послужили основой, наряду с другими работами учеников и последователей Н.Н. Павловского, для создания инженерной гидравлики, широко используемой при расчетах в гидротехнике.
Труды академика Н.Н. Павловского (1884 – 1937) в области равномерного и неравномерного движения, фильтрации через земляные плотины и под гидротехническими сооружениями явились большим вкладом в развитие гидравлики и послужили основой, наряду с другими работами учеников и последователей Н.Н. Павловского, для создания инженерной гидравлики, широко используемой при расчетах в гидротехнике.
3. ЦЕЛЬ ПРЕПОДАВАНИЯ ДИСЦИПЛИНЫ
Дидактическая цель курса заключается в формировании у студентов теоретических и прикладных знаний необходимых для изучения специальных курсов по специальности «Проектирование, сооружение и эксплуатация газонефтепроводов и газонефтехранилищ», а также для решения многих инженерных задач.
Целью преподавания является подготовка специалиста для производственно-технической, организационно-управленческой, проектно-конструкторской и исследовательской деятельности в области проектирования, сооружения и эксплуатации газонефтепроводов и газонефтехранилищ.
4. ЗАДАЧИ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ
Задачами изучения дисциплины являются:
1. Теоретическая подготовка в области гидромеханики, позволяющая будущим инженерам ориентироваться в потоке научно-технической информации и обеспечивающая возможность использования ими гидромеханических методов в будущей специальности.
2. Формирование у студентов научного мышления в частности, правильного понимания границ применяемости различных гидромеханических понятий, законов, теорий и умение оценивать степень достоверности результатов, полученных с помощью экспериментальных и математических методов исследования или инженерных расчетов.
3. Усвоение основных гидромеханических явлений и законов, методов гидромеханических исследований применительно к различным задачам будущей специальности.
4. Выработка у студентов приемов и навыков решения конкретных задач из разных областей гидромеханики, помогающих студентам в дальнейшем решать инженерные задачи.
Настоящий учебно-методический комплекс составлен на основе различных учебников, учебных и учебно-методических пособий и предназначен для использования студентами специальности 1-70 05 01 «Проектирование, сооружение и эксплуатация газонефтепроводов и газонефтехранилищ» при изучении дисциплины «Техническая гидромеханика» на кафедре трубопроводного транспорта и гидравлики.
Перечни литературных источников, которые были использованы при составлении учебно-методического комплекса, приводятся в конце каждого модуля.
МОДУЛЬ 1
ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТИ
1. ВВЕДЕНИЕ
Жидкостью называется физическое тело, обладающее весьма большой подвижностью частиц. В то время как для изменения формы твердого тела к нему нужно приложить конечные, иногда очень большие силы, изменение формы жидкости может происходить под действием даже самых малых сил. Жидкость сильно деформируется, не дробясь на частицы. Говорят, что она обладает текучестью. Деформация происходит даже под воздействием собственного веса, поэтому жидкость изменяет форму в сосуде, в котором она находится.
Жидкость, как и всякое физическое тело, имеет молекулярное строение, то есть состоит из отдельных частиц-молекул, объем пространства между которыми во много раз превосходит объем самих молекул.
Однако из-за чрезвычайной малости не только самих молекул, но и расстояний между ними (по сравнению с объемами, рассматриваемыми при изучении равновесия и движения жидкости) в механике жидкости ее молекулярное строение не рассматривается; предполагается, что жидкость заполняет все пространство, без образования каких либо пустот. Тем самым, вместо самой жидкости изучается ее модель, обладающая свойством непрерывности (эта модель реализует гипотезу, согласно которой жидкость представляет собой материальный континуум, то есть заполняет пространство сплошным образом).
Эта гипотеза упрощает исследование, так как позволяет рассматривать все механические характеристики жидкой среды (скорость, плотность, давление и т.д.) как функции координат точки в пространстве и времени, причем в большинстве случаев эти функции предполагаются непрерывными и дифференцируемыми.
Эту модель можно использовать до тех пор, пока в достаточно малых объёмах жидкости содержится большое количество молекул. К примеру, в кубике воздуха со стороной размером 0, 001 мм находится 2, 7 × 107 молекул.
Жидкости с точки зрения механических свойств разделяются на два класса: малосжимаемые (капельные) и сжимаемые (газообразные).
Благодаря наличию в капельной жидкости некоторых сил молекулярного взаимодействия, величина их объема мало изменяется под действием внешних сил, то есть они мало сжимаемы. При атмосферном давлении сжимаемость воды в 14000 раз меньше сжимаемости воздуха.
Несмотря на различия молекулярных структур газов и капельных жидкостей, с точки зрения законов их движения между ними во многих случаях нет различия. Исследования показывают, что формулы гидромеханики, выведенные для несжимаемых жидкостей, справедливы и для газов, если скорость их движения не превосходит некоторого предела. Этот предел зависит от отношения скорости движения газа и скорости распространения звука. При величине отношения меньше 0, 2 возможная погрешность в определении давления газа по формулам для несжимаемой жидкости составляет не более 1 %.
Поскольку скорость распространения звука в воздухе ~ 350 м/сек, то при скоростях 70 – 75 м/сек законы движения капельных и газообразных жидкостей можно считать общими.
2. ОСНОВЫ НАУЧНО-ТЕОРЕТИЧЕСКИХ ЗНАНИЙ ПО МОДУЛЮ
2.1. Вязкость жидкости. Формула Ньютона
Любая реальная жидкость и газ обладают свойством вязкости. Вязкость является одной из причин, вызывающей сопротивление течению жидкости по трубам и каналам (внутренняя задача гидромеханики) и движению твердого тела в жидкости (внешняя задача гидромеханики).
Между слоями в потоке вязкой жидкости действуют силы, касательные к направлению их движения. При этом слои жидкости, расположенные ближе к стенке, подтормаживают верхние слои, что приводит к характерному виду эпюры скорости, изображенной на рис. 1.1.
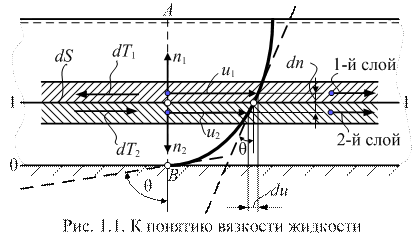
Рис. 1.1. К понятию вязкости жидкости
Силы трения, возникающие между движущимися друг относительно друга слоями жидкости с площадью соприкосновения dS (рис. 1.1), можно определить на основании формулы Ньютона:
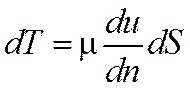 (1.1)
(1.1)
или, если отнести силу трения к площадке dS и обозначить получаемое при этом касательное напряжение через 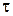 ,
,
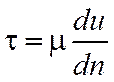 . (1.2)
. (1.2)
(1.2)
В этой формуле 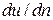 – производная, характеризующая изменение скорости в поперечном к слою направлении, которая согласно рис. 1.1
– производная, характеризующая изменение скорости в поперечном к слою направлении, которая согласно рис. 1.1 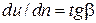 ,
, 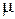 – динамический коэффициент вязкости, зависящий от свойств жидкости. Формула (1.2), предложенная Ньютоном вначале в качестве гипотезы и подвергавшаяся в дальнейшем тщательной опытной проверке, в настоящее время общепринята в гидромеханике для расчета касательных напряжений при ламинарном течении жидкостей и именуется формулой ньютона (законом внутреннего трения Ньютона).
– динамический коэффициент вязкости, зависящий от свойств жидкости. Формула (1.2), предложенная Ньютоном вначале в качестве гипотезы и подвергавшаяся в дальнейшем тщательной опытной проверке, в настоящее время общепринята в гидромеханике для расчета касательных напряжений при ламинарном течении жидкостей и именуется формулой ньютона (законом внутреннего трения Ньютона).
Ламинарным, то есть слоистым, называется течение вязкой жидкости, при котором отсутствует перемешивание между ее слоями. Неупорядоченное движение вязкой жидкости с интенсивным перемешиванием частиц называется турбулентным. В случае турбулентного течения формула Ньютона неприменима.
Динамический коэффициент вязкости m зависит от рода жидкости, ее температуры и (в малой степени) от давления. Размерность m согласно (1.2) [μ ] = ML –1 T –1.
В системе единиц СИ размерность [m] = Н сек м-2, а в технической [m]= кГ сек м-2.
Широкое применение в гидромеханике находит также кинематический коэффициент вязкости n, представляющий отношение m к плотности жидкости r.
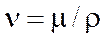 .
.
Размерность [ 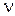 μ ] = L 2 T –1, откуда следует, что в коэффициент
μ ] = L 2 T –1, откуда следует, что в коэффициент 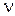 не входят динамические характеристики.
не входят динамические характеристики.
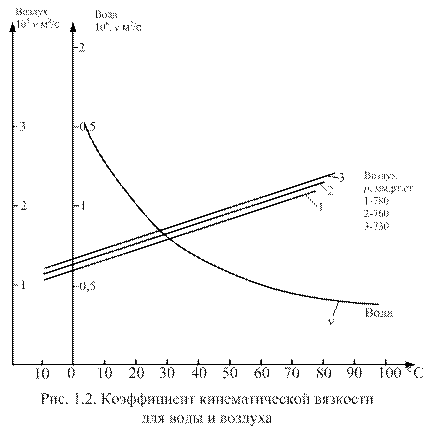
На рис. 1.2 показаны зависимости кинематического коэффициента 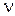 в функции от температуры – для воды и в функции от температуры и давления – для воздуха. Как видно из рисунка, для воды этот коэффициент примерно на порядок меньше, чем для воздуха. Это означает, что вода относительно менее вязкая жидкость, нежели воздух. Коэффициенты вязкости m и n определяются опытным путем.
в функции от температуры – для воды и в функции от температуры и давления – для воздуха. Как видно из рисунка, для воды этот коэффициент примерно на порядок меньше, чем для воздуха. Это означает, что вода относительно менее вязкая жидкость, нежели воздух. Коэффициенты вязкости m и n определяются опытным путем.
Выясним физическую причину возникновения вязкости на примере газа; для этого необходимо учесть его молекулярное строение. Молекулы движущегося газа совершают хаотическое тепловое движение, перескакивая из слоя в слой. При этом происходит обмен количеством движения между слоями.
Между слоями, согласно закону изменения количества движения, возникают силы, которые имеют характер сил сопротивления (трения). Этот обмен количествами движения совершается на «молекулярном уровне». Таким образом, вязкость обусловливается наличием молекулярного движения газа.
Вводя коэффициент вязкости 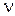 , как физическую характеристику жидкости и тем самым косвенно учитывая действие этого молекулярного движения в газе, можно в дальнейшем по-прежнему использовать гипотезу сплошности для вязкой жидкости, не прибегая к прямому учету молекулярных взаимодействий.
, как физическую характеристику жидкости и тем самым косвенно учитывая действие этого молекулярного движения в газе, можно в дальнейшем по-прежнему использовать гипотезу сплошности для вязкой жидкости, не прибегая к прямому учету молекулярных взаимодействий.
Касательное напряжение равно нулю, если μ = 0, то есть если жидкость лишена свойств вязкости. Второй фактор, определяющий наличие касательных напряжений в жидкости, связан с существованием изменения скорости по нормали (градиент скорости). Если 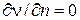 , то τ = 0 даже в вязкой жидкости.
, то τ = 0 даже в вязкой жидкости.
Жидкости, подчиняющиеся закону внутреннего трения Ньютона, называются нормальными, или ньютоновскими. К ним относятся наиболее важные жидкости и газы, такие, как вода, воздух, нефтепродукты, ртуть и др.
Жидкости, в которых связь между напряжениями и градиентами скоростей не подчиняется формуле (1.2), называются аномальными, или неньютоновскими. К ним относятся некоторые смазочные масла при низких температурах, коллоидные растворы, масляные краски, глинистые растворы, а также растворы в воде некоторых высокомолекулярных соединений. Движение подобных аномальных жидкостей исследуется в реологии, а также в специальных разделах гидромеханики.
2.2. Плотность жидкости
Для характеристики распределения массы в пространстве, заполненном жидкостью или газом, обычно пользуются величиной, называемой плотностью распределения массой или, чаще, плотностью.
Среднее значение плотности среды в некотором малом объеме определяется по отношению массы 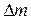 , заключенной в этом объеме, к самому объему
, заключенной в этом объеме, к самому объему 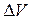 :
:
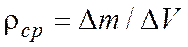 .
.
Часто пользуются не средним значением плотности вещества в некотором объеме, а величиной плотности среды в данной точке M, в которой
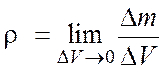 .
.
При этом точка М при 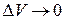 всегда остается внутри
всегда остается внутри 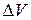 .
.
Иногда для характеристики распределения массы в пространстве применяют величину, обратную плотности, называемую удельным объемом 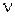 .
.
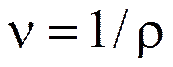 .
.
Плотность движущейся среды зависит от температуры и давления, а последнее – от характера движения среды.
В общем случае плотность можно представить как функцию от координат и времени
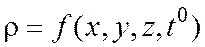 .
.
В технике пользуются понятием удельного веса 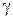 определяемым как отношение силы тяжести, действующей на объем жидкости к величине этого объема (сила тяжести F приходящаяся на единицу объема жидкости):
определяемым как отношение силы тяжести, действующей на объем жидкости к величине этого объема (сила тяжести F приходящаяся на единицу объема жидкости):
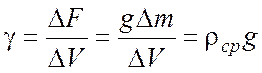 ;
;
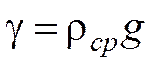 .
.
Размерность плотности:
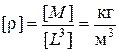 .
.
Размерность удельного веса:
; 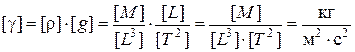 .
.
2.3. Сжимаемость
Способность жидкости или газа под действием внешнего давления изменять свой объем и, следовательно, плотность, называется сжимаемостью. Сжимаемость жидкости характеризуется коэффициентом объемного сжатия (сжимаемости) bс, м2/Н, представляющим относительное изменение объема жидкости V, м3, при изменении давления р, Па, на единицу:
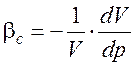 .
.
Знак минус в формуле указывает, что при увеличении давления объем жидкости уменьшается.
Величина, обратная коэффициенту объемного сжатия – модуль упругости жидкости:
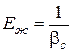 .
.
При относительно невысоких давлениях сжимаемостью жидкостей пренебрегают. При значительных изменениях давления сжимаемость капельных жидкостей следует учитывать.
Вследствие большой сжимаемости газообразных жидкостей их плотность и удельный вес в значительной степени зависят от температуры и давления.
Процессы сжатия и расширения газов подчиняются известным из физики законам Бойля – Мариотта и Гей – Люссака для идеальных газов.
Сжимаемость воды весьма незначительна, при увеличении давления на 9, 8 МПа (на 100 атмосфер) объем воды уменьшается на 1/20000 первоначального объема.
Условия работы гидротехнических сооружений позволяют считать воду несжимаемой средой. Но не следует забывать, что такое допущение правомерно лишь в тех случаях, когда изменения давления невелики.
2.4. Поверхностное натяжение (капиллярность)
Известно, что молекулы жидкости, находящиеся на границе с газом, твердым телом или между двумя несмешивающимися жидкостями, находятся под воздействием сил взаимного притяжения. Вследствие этого вся свободная поверхность жидкости находится в состоянии равномерного поверхностного натяжения s. Под влиянием поверхностного натяжения поверхность жидкости стремится принять форму, соответствующую наименьшей площади. Малые массы жидкости в воздухе стремятся к шарообразной форме, образуя капли.
Влияние поверхностного натяжения необходимо учитывать при изучении потоков с малой глубиной, при захвате окружающего воздуха движущейся жидкостью (аэрация жидкости), в капиллярах и т.д.
В трубках малого диаметра наблюдается подъем или опускание жидкости относительно нормального уровня, а также искривление свободной поверхности. Обратимся к рассмотрению жидкости в капиллярной трубке. Как видно из рис. 1.3, в районе примыкания поверхности жидкости к стенке трубки можем получить одну из следующих картин:
- если взаимное притяжение двух молекул жидкости велико по сравнению с притяжением молекул жидкости к частице твердой стенки, то получаем схему рис. 1.3, а (случай «несмачиваемой стенки»);
- если взаимное притяжение двух молекул жидкости мало по сравнению с притяжением молекул жидкости к частице твердой стенки, то получаем схему на рис. 1.3, б (случай «смачиваемой стенки»).
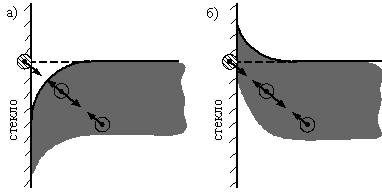
Рис. 4.1. «Несмачиваемая» (а) и «смачиваемая» (б) стенки
Высота подъема смачивающей жидкости (или опускание несмачивающей жидкости) в стеклянной трубке диаметром d определяется по формуле для полусферического мениска:
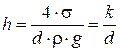 ,
,
где k имеет следующие значения: для воды k = 30 мм2; для ртути
k = – 10, 1 мм2; для спирта k = 11, 5 мм2.
Величина напряжений на границе раздела зависит от температуры жидкости; при увеличении температуры внутренняя энергия молекул возрастает, уменьшается напряжение в пограничном слое жидкости и, следовательно, уменьшаются силы поверхностного натяжения.
2.5. Растворимость газов в капельных жидкостях
В реальных жидкостях всегда находится газ в растворенном состоянии. Это может быть воздух, азот, углеводородный газ, углекислота, сероводород и др. Наличие газа растворенного в жидкости может оказывать как благоприятное воздействие (снижается вязкость жидкости, плотность и т.д.), так и неблагоприятные факторы. Так при снижении давления из жидкости выделяется свободный газ, который может стать источником такого нежелательного явления как кавитация.
Количество газа, которое может раствориться в капельной жидкости, зависит от физико-химических свойств самой жидкости и растворяемого в ней газа, а также от температуры и давления. Максимальное количество газа, которое может быть растворено в данной жидкости носит название предельной газонасыщенности для данного газа SО. Естественно, что величины предельной газонасыщенности для разных газов будут разными. Другой характеристикой процесса растворения газа в жидкости является давление насыщенных паров рн.п, это такое минимальное давление в жидкости, при котором достигается насыщение капельной жидкости газом. Известно, что рн.п. зависит от температуры и с увеличением ее повышается.
Если давление в жидкости р опустится ниже давления насыщенных паров (р < рн.п), то растворенные в жидкости газы начнут из нее выделяться в виде пузырьков.
2.6. Кипение и кавитация
Как известно из курса физики, при снижении давления в жидкости или при повышении ее температуры растворенные в воде газы начинают выделяться из отдельных элементарных объемов воды, причем в воде образуются разрывы (газовоздушные пузыри).
Предположим, что мы имеем некоторый объем воды, сплошность которого не нарушена. Обозначим давление в этой воде через р и температуру через t.
Представим себе далее, что в силу тех или иных причин температура начинает увеличиваться или давление уменьшаться. Очевидно, что в некоторый момент времени можем получить р < рн.п. При таком соотношении в обычных условиях внутри рассматриваемого объема воды возникают пузырьки, заполненные «насыщенными парами» воды, происходит, как говорят «холодное кипение» воды. При этом мы получаем двухфазную систему (вода плюс пузырьки пара). Чтобы заставить эти пузырьки захлопнуться необходимо на достаточную величину или повысить давление р или понизить давление рп.н. (за счет снижения температуры).
В случае появления в воде пузырьков пара различают два разных явления: кипение и кавитацию.
3. СЛОВАРЬ ПОНЯТИЙ
Плотностью называется величина, используемая для характеристики распределения массы в пространстве, заполненном жидкостью или газом.
Сжимаемостью называется способность жидкости или газа под действием внешнего давления изменять свой объем и, следовательно, плотность.
Кипением жидкости называется явление, когда пузырьки пара, появившиеся в жидкости всплывают и выходят из жидкости через ее свободную поверхность.
Кавитацией жидкости называется явление, когда пузырьки пара (или паровоздушные пузырьки), появившиеся в движущейся жидкости, не выходят из нее, а захлопываются внутри жидкости.
4. МАТЕРИАЛЫ, ИСПОЛЬЗУЕМЫЕ В ПРОЦЕССЕ ОБУЧЕНИЯ
4.1. Материалы к лекции
Возможен следующий план лекции:
1. Вязкость жидкости. Формула Ньютона.
2. Плотность жидкости.
3. Сжимаемость.
4. Поверхностное натяжение (капиллярность).
5. Растворимость газов в капельных жидкостях.
6. Кипение и кавитация.
4.2. Задание к практическому занятию
ЛАБОРАТОРНАЯ РАБОТА № 1.
«ОПРЕДЕЛЕНИЕ ВЯЗКОСТИ ЖИДКОСТИ
ВИСКОЗИМЕТРОМ ЭНГЛЕРА»
Цель работы:
1. Определить динамическую вязкость исследуемой жидкости с помощью вискозиметра Энглера.
2. Установить зависимость вязкости исследуемой жидкости от температуры.