Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства напряжений внутренних сил, действующих в жидкости
|
|
Для исследования напряжений внутренних сил в жидкости установим связь между напряжением, действующим на произвольно ориентированную площадку и три другие взаимно перпендикулярные площадки, проходящие через данную точку.
Выделим в движущейся жидкости элементарную жидкую частицу в форме тетраэдра (рис. 2.3). Вместо поверхностных сил на гранях тетраэдра изображены векторы напряжений, направленные произвольным образом к соответствующим граням.
Ускорение центра тяжести частицы обозначим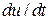 
, напряжение массовых сил – F. Напишем уравнение движения этой элементарной частицы в векторной форме:
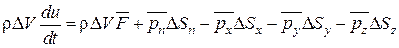, (2.12)
где ∆ Sx, ∆ Sy и ∆ SZ – площади граней тетраэдра, перпендикулярные соответствующим осям координат;
pn, рх, ру, рz – векторы напряжений в центре площадок, обозначения которых соответствуют направлению нормалей к ним; знаки минус перед последними членами означают, что нормали к соответствующим площадкам направлены противоположно осям координат.
Из аналитической геометрии известно, что
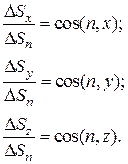(2.13)
Разделим обе части уравнения (2.12) на ∆ Sn и используем (2.13):
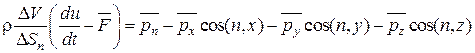. (2.14)
Чтобы получить связь между напряжениями в точке, устремим объем тетраэдра к нулю, стягивая его в точку к началу координат. Очевидно, что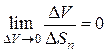 
, с учетом чего связь между напряжениями запишется в виде:
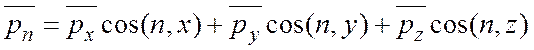. (2.15)
Проектируя рп на оси координат, получим:
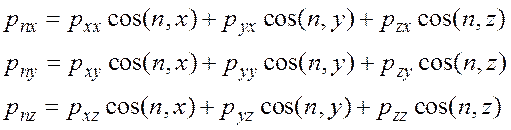
Первый индекс при проекциях напряжений в этих соотношениях соответствует площадке, в которой действует данное напряжение, а второй – оси, на которую оно проектируется. Скалярные величины рхх, руу, pzz представляют нормальные напряжения, а рху, рхz, – касательные напряжения, действующие в определенных площадках.
В дальнейшем будем обозначать касательные напряжения буквой τ:
pxy = τ xy; pxz = τ xz; py z = τ yz,
учитывая это, перепишем в виде:
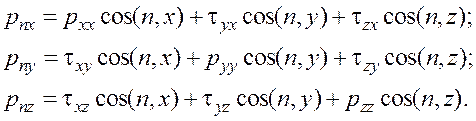
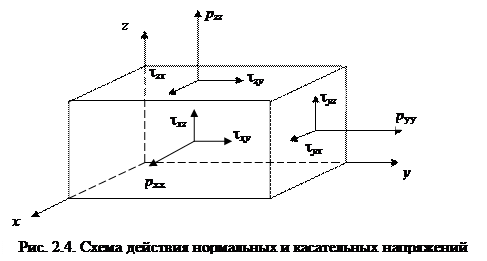
Нормальные и касательные напряжения, действующие на три взаимно перпендикулярные грани параллелепипеда, выделенного в жидкости, показаны на рис. 2.4. Применяя теорему моментов, взятых относительно начала координат для напряжений, действующих на грани параллелепипеда, легко доказать свойство взаимности касательных напряжений, в соответствии с которым
τ xy = τ yx, τ zx = τ xz, τ yz = τ zy.
Такие величины в математике и механике носят название тензора, таким образом первое свойство напряжений поверхностных сил состоит в том, что эти напряжения образуют тензор напряжений.
.
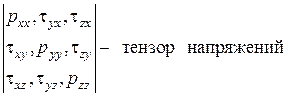На основании изложенного можно сделать вывод, что напряжения внутренних сил в данной точке жидкости, то есть напряженное состояние жидкости, характеризуются совокупностью девяти скалярных величин, образующих так называемый тензор напряжений. Вследствие свойства взаимности число независимых величин в нем сокращается до 6.
Выясним основные свойства напряжений в жидкости.
Возникновение в жидкости касательных напряжений τ xy, τ xz, τ yz вызвано одновременным влиянием двух факторов: движения жидкости и ее вязкости.
Если жидкость неподвижна, то касательные напряжения в ней отсутствуют, что характерно как для вязкой, так и для невязкой жидкости. Таким образом, в покоящейся (вязкой и невязкой) и в движущейся невязкой жидкости:
τ xy = τ xz = τ yz = 0,
то есть действуют только нормальные напряжения рхх, руу, рzz. Соответствующие векторы напряжений:
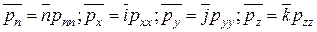. (2.16)
Подставляя в уравнение, получим:
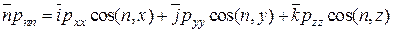. (2.17)
Известно, что
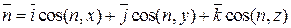. (2.18)
Подставим (2.18) в левую часть (2.17):
.
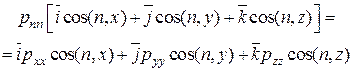Сравнивая в этом выражении коэффициенты при одинаковых ортах, найдем
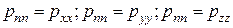(2.19)
или
. (2.20)
Эти равенства позволяют сформулировать теорему о свойстве нормальных напряжений: если в жидкости отсутствуют касательные напряжения, то нормальное напряжение в данной точке не зависит от ориентации площадки. Зависимость (2.20) выполняется при покое вязкой жидкости и при движении и покое невязкой жидкости.
Рассмотрим одно из основных свойств жидкости, связанное с нормальными напряжениями. Как видно из рис. 2.4, рхх, руу, рzz направлены в сторону внешней нормали, то есть нормальные напряжения – растягивающие, которым приписывается знак плюс.
Твердое тело одинаково воспринимает растягивающие и сжимающие нормальные напряжения, не меняя своего состояния; в нем при этом не образуется разрывов сплошности (пустот). Капельная жидкость, как показывает опыт, способна воспринять произвольные сжимающие усилия (отрицательные нормальные напряжения) без разрыва сплошности. Однако опыт показывает, что жидкость практически терпит разрыв при растяжении, то есть в ней могут проявляться лишь нормальные сжимающие усилия, называемые давлениями.
Назовем давлением р в жидкости при отсутствии касательных напряжений величину нормального напряжения, взятую с обратным знаком; тогда в соответствии с (2.20):
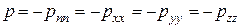, (2.21)
откуда следует, что величина давления не зависит от ориентации площадки.
Давление (и вообще напряжение) в системе единиц МКГСС измеряют в кГ/м2; его часто измеряют также в технических атмосферах (т.а):
1 т.а = 1 кГ/см2 = 10000 кГ/м.
В системе единиц СИ давление принято измерять в ньютонах на квадратный метр:
1 кГ/м2 = 9, 806 н/м2.
Согласно (2.16) нормальное напряжение выражается через давление зависимостями:
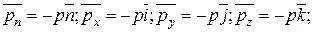(2.22)
где знак минус указывает, что нормальное напряжение в жидкости всегда направлено противоположно внешней нормали и является сжимающим напряжением.
Давление в жидкости без нарушения ее сплошности, как показывает опыт, не падает ниже давления рн насыщенных паров
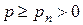. (2.23)
Приведенное выше определение давления справедливо для покоящейся вязкой и невязкой жидкости, а также для движущейся невязкой жидкости. Отметим, что данное выше определение давления может с достаточной степенью точности применяться и при изучении движения маловязкой жидкости, например воды или воздуха.