
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание № 3. исследовать заданную функцию методами дифференциального исчисления и построить эскиз графика.
|
|
исследовать заданную функцию методами дифференциального исчисления и построить эскиз графика.
у=2х3-9х2+12х-5,
Точки пересечения с осью координат X
| График функции пересекает ось X при f = 0 | ||||||
| значит надо решить уравнение: | ||||||
| 3 2 2*x - 9*x + 12*x - 5 = 0 | ||||||
| Точки пересечения с осью X: | ||||||
| Аналитическое решение | ||||||
| x1 = 1 | ||||||
| x2 = 5/2 | |||
| Численное решение | |||
| x1 = 0.999999433856 | |||
| x2 = 2.5 | |||
и координат Y
| График пересекает ось Y, когда x равняется 0: | ||
| подставляем x = 0 в 2*x^3 - 9*x^2 + 12*x - 5. | ||
| 3 2 2*0 - 9*0 + 12*0 - 5 | ||
| Результат: | |||||
| f(0) = -5 | |||||
| Точка: | |||||
| (0, -5) | |||||
| f = 2*x^3 - 9*x^2 + 12*x - 5 | |||||
стремумы функции
| Для того, чтобы найти экстремумы, | |||||||||||||||||||||||
| нужно решить уравнение | |||||||||||||||||||||||
| d --(f(x)) = 0 dx | |||||||||||||||||||||||
| (производная равна нулю), | |||||||||||||||||||||||
| и корни этого уравнения будут экстремумами данной функции: | |||||||||||||||||||||||
| d --(f(x)) = dx | |||||||||||||||||||||||
| 12 - 18*x + 6*x = 0 | |||||||||||||||||||||||
| Решаем это уравнение | |||||||||||||||||||||||
| Корни этого ур-ния | |||||||||||||||||||||||
| x1 = 1 | |||||||||||||||||||||||
| x2 = 2 | |||||||||||||||||||||||
| Зн. экстремумы в точках: | |||||||||||||||||||||||
| (1, 0) | |||||||||||||||||||||||
| (2, -1) | |||||||||||||||||||||||
| Интервалы возрастания и убывания функции: | |||||||||||||||||||||||
| Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума: | |||||||||||||||||||||||
| Минимумы функции в точках: | |||||||||||||||||||||||
| x2 = 2 | |||||||||||||||||||||||
| Максимумы функции в точках: | |||||||||||||||||||||||
| x2 = 1 | |||||||||||||||||||||||
| Убывает на промежутках | |||||||||||||||||||||||
| (-oo, 1] U [2, oo) | |||||||||||||||||||||||
| Возрастает на промежутках | |||||||||||||||||||||||
| [1, 2] | |||||||||||||||||||||||
Точки перегибови фунии

Задание № 4
вычислить неопределенные интегралы, результат проверить дифференцированием.
а) 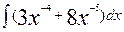 =
= 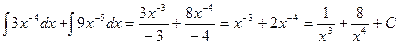 ;
;
б) 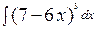 .
.
Задание № 5
вычислить площадь фигуры, ограниченную заданными линиями:
31. y=x2, y=49.
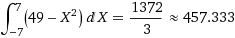

Задание № 6
выполните арифметические действия над комплексными числами: z1 и z2
z1 = 3-5 i и z2= -3+4 i
Задание № 7