Найдем выборочное уравнение линейной регрессии

На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.

Линейное уравнение регрессии имеет вид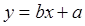

Система нормальных уравнений имеет вид:

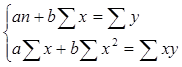
Наша система уравнений имеет вид:

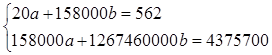
Решим ее методом Крамера

;

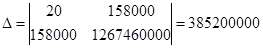
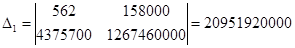
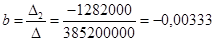
Получаем эмпирические коэффициенты регрессии:

b = –0, 00333, a =54, 3923

Уравнение регрессии:

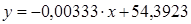
Описание уравнения регрессии

Коэффициентам уравнения линейной регрессии можно придать экономический смысл.

Коэффициент регрессии b = –0, 00333 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y понижается в среднем на –0, 00333.

Коэффициент a = 54, 3923 формально показывает прогнозируемый уровень у, но только в том случае, если х =0 находится близко с выборочными значениями.

Но если х =0 находится далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.

Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя y (x) для каждого наблюдения.

Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе – обратная). В нашем примере связь обратная.