
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Приведение задачи линейного программирования от одной эквивалентной формы к другой
|
|
1. Сведение задачи минимизации к задаче максимизации:
Преобразование сводится к смене знака критерия.
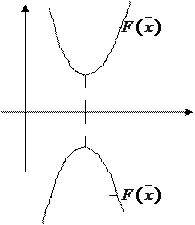 |
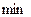
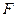 (
(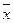 ) ~
) ~ 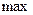 (
( (
(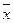 ))
))
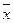
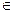
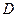
|
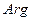
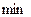
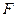 (
(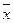 ) =
) = 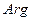
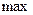 (
( (
(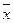 ))
))
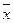
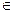
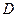
2. Переход от ограничений-неравенств к уравнениям:
· 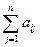
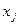
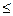
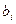 (20)
(20)
Неравенство (20) заменяется на уравнение (21) и условие (22)
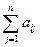
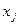 +
+ 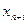 =
= 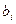 (21)
(21)
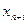
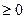 (22)
(22)
Переменные 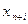 – дополнительные или балансовые, так как обеспечивают баланс правой и левой частей.
– дополнительные или балансовые, так как обеспечивают баланс правой и левой частей.
·
|
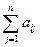
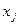
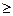
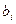
Аналогично, неравенство (23) заменяется на уравнение (24) и условие (25)
|
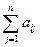
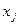 -
- 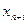 =
= 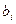
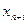
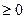
3. Переход от переменных произвольного знака к неотрицательным переменным:
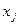 =
= 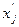 -
- 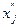
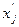
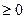
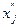
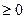
4. Переход от переменных, ограниченных снизу, к неотрицательным:
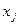
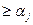
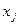 =
= 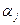 +
+ 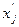
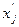
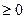
5. Переход от уравнений к неравенствам:
· Если имеется уравнение:
|
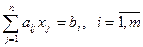
|
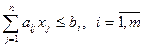
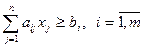
· Пусть есть несколько ограничений:
|
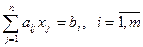
|
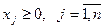

Пусть ранг (количество линейно-независимых уравнений) системы ограничений равен 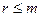 , тогда
, тогда 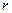 переменных можно выразить через остальные:
переменных можно выразить через остальные:
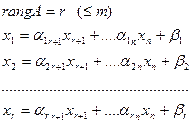
|
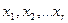 – базисными переменными.
– базисными переменными.
Задавая произвольные значения свободным переменным, получаем частные решения, но не все они удовлетворяют условиям неотрицательности:
|
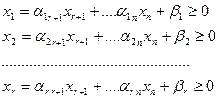
Тогда для свободных переменных получаем ограничения в виде неравенств:
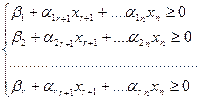
Если (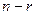 ) = 2, то задача допускает иллюстрацию в пространстве двух переменных.
) = 2, то задача допускает иллюстрацию в пространстве двух переменных.
 Для задачи в канонической форме, если все уравнения независимы и переменных на две больше, чем уравнений (т.е. (
Для задачи в канонической форме, если все уравнения независимы и переменных на две больше, чем уравнений (т.е. ( ) = 2), то свободных переменных в общем решении будет две и задача допускает графическое решение.
) = 2), то свободных переменных в общем решении будет две и задача допускает графическое решение.