Векторное представление симплексных преобразований

Пусть имеется опорный план 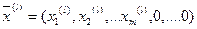и он невырожденный.

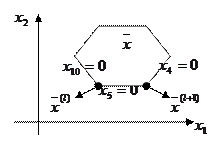
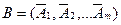- базисная матрица.

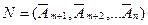- небазисная матрица.

Рассмотрим произвольное допустимое решение (это не угловая точка):

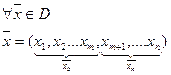
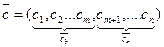
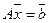, подставим в условие (2).

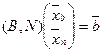
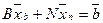
Выразим базисные переменные через свободные и найдем общее решение системы уравнений:

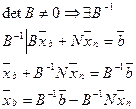
Рассмотрим критерий на произвольном решении :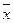

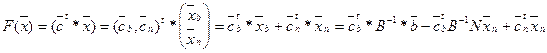
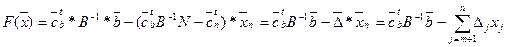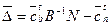
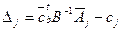
На опорном плане 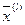свободные переменные равны нулю, поэтому

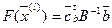а критерий в произвольной точке области выразится через свободные переменные в виде

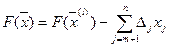
Теорема 4: Опорный план 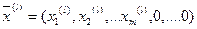задачи ЛП является оптимальным, если все оценки свободных переменных неотрицательны, т.е. .

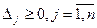Доказательство:

Для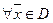

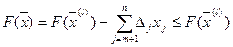
т.к. 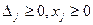, то и .

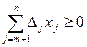Значит решение 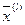оптимальное, так как во всех точках области значение критерия меньше (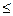), чем критерий в точке .

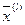Теорема доказана.