Математическое описание вибраторных антенных решеток

Для проектирования антенных решеток и оптимизации их характеристик необходимо наличие точной и высокоэффективной в вычислительном отношении математической модели, поскольку многоэлементные ВК имеют большое число степеней свободы (длины вибраторов, расстояние между ними). Математическое описание можно свести к системе связанных интегральных уравнений относительно неизвестных функций распределения тока в каждом элементе.

6.2.1. Система связанных интегральных уравнений
для многоэлементной антенной решетки ВК

Математическая модель ВК сводится к системе связанных интегральных уравнений, порядок которой совпадает с количеством элемента. Например, для пятиэлементной антенны, представленной на рис. 6.6. искомыми являются пять функций распределения токов в рефлекторе, активном элементе и трех директорах.

Основываясь на тех же допущениях, что и при выводе уравнения По­клингтона одиночного вибратора (т. е. наличие сильного скин-эффекта, приближение тонкого провода) [1], можно сформулировать систему уравнений относительно неизвестных токов на каждом элементе ВК:

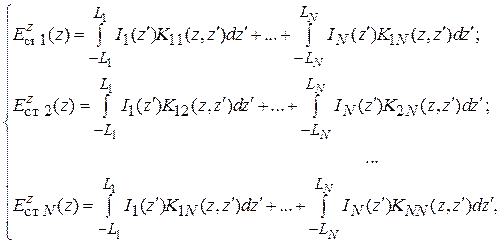(6.1)

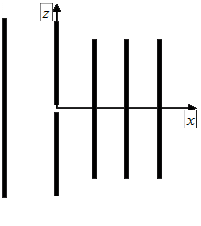где 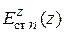– стороннее электрическое поле (продольная компонента), создаваемое внешним источниками поля, 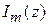– ток, протекающий по оси m -го элемента. Ядра системы (6.1) определяются на основе соотношений:

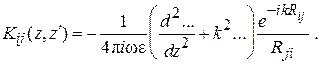(6.2)

Здесь – 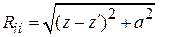– расстояние между точкой интегрирования на оси и точкой наблюдения на поверхности i -го вибратора,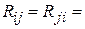 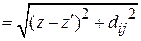– расстояние между точкой интегрирования на оси i -го вибратора и точкой наблюдения на поверхности j -го вибратора, из (6.2) видно, что: .

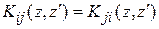В случае одного активного элемента левые части системы уравнений (6.1) имеют вид:

Значения стороннего электрического поля во всех строчках системы, кроме второй, равняются нулю, что объясняется наличием возбуждающего источника лишь у второго элемента.

Физический смысл системы интегральных уравнений (6.1) заключается в том, что каждая строчка – это запись граничного условия для касательной компоненты электрического поля на поверхности вибратора. Интегралы в правой части любой строки системы (6.1) – это вклад в поле на поверхности одного из вибраторов от каждого из N элементов антенной решетки, таким образом, общее число интегралов в системе равно квадрату числа элементов решетки.

Полученная система (6.1) описывает в самосогласованной постановке систему из N вибраторов с учетом взаимного влияния их друг на друга. В частном случае, при отсутствии взаимной связи (например, в случае значительного междуэлементного расстояния, т. е. при 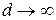), ядра системы (6.1) стремятся к нулю. Легко убедиться, что в этом случае система распадается на N независимых систем относительно тока в каждом уединенном вибраторе (т.е. на N независимых уравнений Поклингтона).