Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение системы связанных ИУ
|
|
Система (6.1) является обобщением уравнения Поклингтона для одиночного элемента и решается в пять этапов:
1-й этап. Выбираем систему базисных функций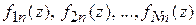 
по которым раскладывается предполагаемое решение на первом, втором и
N -м вибраторах.
При этом возможна ситуация, в которой число базисных функций на каждом вибраторе неодинаково: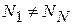 
, а их вид на разных вибраторах разный. Получается система уравнений
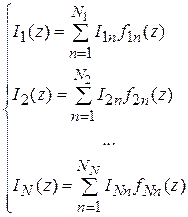(6.3)
2-й этап. Подставляем разложение (6.3) в исходную систему интегральных уравнений (6.1) и, меняя порядок суммирования и интегрирования, получаем:
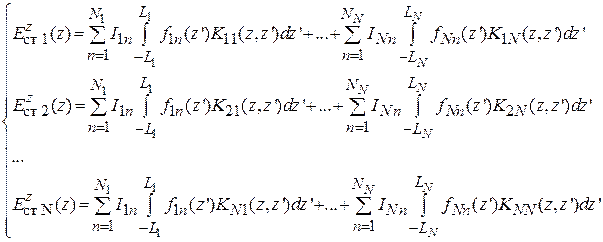
(6.4)
3-й этап. Формируем систему линейных алгебраических уравнений на основе метода Галеркина. На этом этапе конкретизируем и упростим ситуацию, будем считать, что ток на каждом вибраторе описывается тремя базисными функциями. Далее, последовательно умножив правую и левую части уравнений системы (6.4) на проекционные функции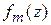 
, получим систему линейных алгебраических уравнений (СЛАУ) M = 3 N порядка относительно неизвестных базисных коэффициентов на каждом вибраторе:
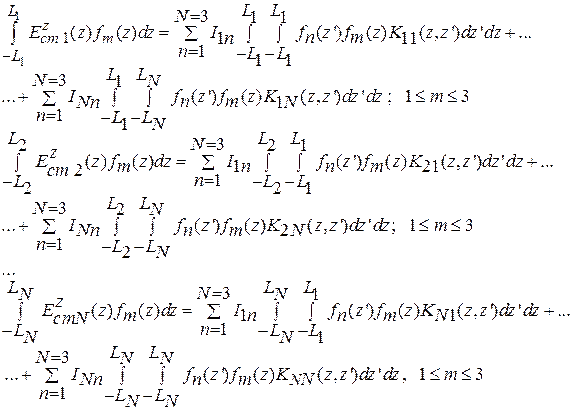(6.5)
Систему (6.5) можно переписать в более наглядном виде, введя сквозную нумерацию базисных функций и токов:
(6.6)
или в матричном виде – [ U ]=[ Z ][ I ]
Здесь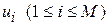 
– амплитуды напряжения, выражаемые через интегралы от напряженности стороннего электрического поля: 
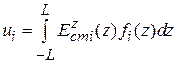, причем вектор-столбец левых частей для ВК имеет вид
,
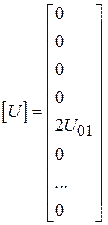где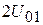 
– напряжение дельта-источника, включенного в центре активного элемента (центральный сегмент активного элемента имеет 5-й порядковый номер), остальные элементы вектора [ U ] равны нулю; элементы матрицы [ Z ] – обобщенных взаимных импедансов 
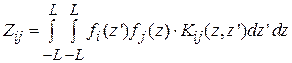; [ I ] – вектор неизвестных базисных коэффициентов.
4-й этап. Решаем систему уравнений (6.6) любым известным способом, например методом Гаусса. В результате решения будут найдены базисные коэффициенты токов.
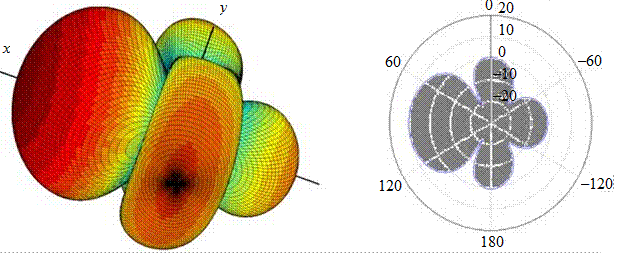
Рис. 6.7
5-й этап. По найденным коэффициентам на основе (6.3) восстанавливается ток в каждом вибраторе, затем находится входное сопротивление активного вибратора и ДН всей системы.
Результаты решения системы и вычисления ДН 5-элементной ВК (рис. 6.6) представлены на рис. 6.7.
Рассмотренный выше частный пример электродинамического анализа проволочных антенн можно легко алгоритмизировать в доступных математических пакетах.
|
|