Краткие теоретические сведения. Решение задач линейного программирования графическим методом

Стр 1 из 4Следующая ⇒

Решение задач линейного программирования графическим методом

Краткие теоретические сведения

В линейной алгебре доказано, что множество допустимых решений (многогранник решений) ЗЛП представляет собой выпуклый многогранник (или выпуклую многогранную область), а оптимальное решение задачи находится, по крайней мере, в одной из угловых точек многогранника решений.

Вершину многогранника решений, в которой целевая функция принимает максимальное (минимальное) значение, определить сравнительно просто, если задача, записанная в стандартной форме, содержит не более двух переменных или задача, записанная в форме основной, содержит не более двух свободных переменных, т. е. n - r £ 2, где n — число переменных, r — ранг матрицы, составленной из коэффициентов в системе ограничений задачи.

Получим решение задачи, состоящей в определении максимального значения функции

F = c₁x₁ + c₂x₂ (2.1)

при условиях

a_i₁x₁ + a_i₂x₂ £ b_i, (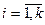) (2.2)

x_j> 0 (j=1, 2). (2.3)

Каждое из неравенств (2.2), (2.3) системы ограничений задачи геометрически определяет полуплоскость соответственно с граничными прямыми a_i₁x₁ + a_i₂x₂ = b_i ( 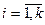), х₁ = 0 и х₂ = 0.

В том случае, если система неравенств (2.2), (2.3) совместна, область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям. Так как множество точек пересечения данных полуплоскостей — выпуклое, то областью допустимых решений задачи (2.2), (2.3) является выпуклое множество, которое называется многоугольником решений (введенный ранее термин «многогранник решений» обычно употребляется, если n ≥ 3). Стороны этого многоугольника лежат на-прямых, уравнения которых получаются из исходной системы ограничений формальной заменой знаков неравенств на знаки точных равенств.

Таким образом, исходная задача линейного программирования состоит в вычислении такой точки многоугольника решений, в которой целевая функция F принимает максимальное значение. Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение.

Для определения данной вершины строят линию уровня c₁х₁+с₂х₂ = h (где h — некоторая постоянная), проходящую через многоугольник решений, и передвигают ее в направлении вектора С = (с₁, с₂) до тех пор, пока она не коснется последней точки многоугольника решений. Координаты указанной точки и определяют оптимальный план данной задачи.

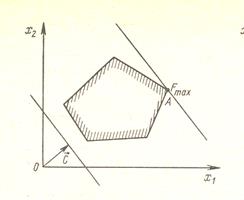
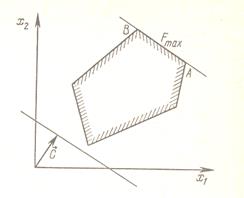
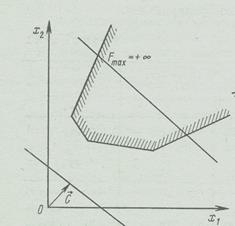
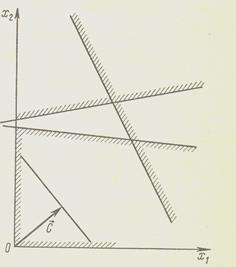
При получении решения могут встретиться случаи, изображенные на рисунке 2.1, a, b, c, d

a) b)

c) d)

Рисунок 2.1 – Возможные варианты решения задачи

Рисунок 2.1, а характеризует такой случай, когда целевая функция принимает максимальное значение в единственной точке А.

Из рисунка 2.1, b следует, что максимальное значение целевая функция принимает в любой точке отрезка АВ.

На рисунке 2.1с изображен случай, когда целевая функция не ограничена сверху на множестве допустимых решений (число решений бесконечно, а оптимального решения нет).

На рисунке 2.1d показан случай, когда система ограничений задачи несовместна (решение отсутствует).

Отметим, что получение минимального значения линейной функции при данной системе ограничений отличается от вычисления ее максимального значения при тех же ограничениях лишь тем, что линия уровня c₁х₁+с₂х₂ = h передвигается не в направлении вектора С =(с₁, с₂), а в противоположном направлении. Таким образом, отмеченные случаи, встречающиеся при определении максимального значения целевой функции, имеют место и при определении ее минимального значения.

Итак, решение решения задачи линейного программирования (2.2), (2.3) на основе ее геометрической интерпретации включает следующие шаги:

1) изображают систему координат (как правило, по оси абсцисс – ось х₁, по оси ординат – ось х₂);

2) строят прямые, уравнения которых получаются в результате формальной замены в ограничениях (2.2), (2.3) знаков неравенств на знаки точных равенств;

3) определяют полуплоскости, определяемые каждым из ограничений задачи;

4) строят многоугольник решений;

5) строят вектор С =(с₁, с₂) (вектор С получается в результате вычисления градиента целевой функции С = { 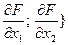. В качестве начальной точки градиента всегда принимают точку начала координат Х⁽⁰⁾(00);

6) строят прямую c₁х₁+с₂х₂ = h, проходящую через любую точку, принадлежащую многоугольнику решений. Эта прямая называется линией уровней;

7) перемещают прямую c₁х₁+с₂х₂ = h в направлении вектора С, в результате чего либо получают точку (точки), в которой целевая функция принимает максимальное значение, либо устанавливают неограниченность сверху функции на множестве планов;

8) определяют координаты точки максимума функции и вычисляют значение целевой функции в этой точке.

Хотя решение задачи с двумя переменными не представляет особого труда, однако, в нем есть ряд моментов, для разрешения которых необходимо владеть определенными приемами.

1.2 Практическая часть.

Решение задачи групповым методом.

1.2.1 Решим следующую экономическую задачу.

Задача 2.1. (задача об использовании ресурсов – задача планирования производства). Метод - коллективное решение задачи.

Для изготовления двух видов продукции P₁ и P₂ предприятие использует четыре вида ресурсов S₁, S₂, S₃, S₄.

Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице 2.1.

Таблица 2.1 – Исходные данные к задаче 1

Вид ресурса Запас ресурса Число единиц ресурсов, затрачиваемых на изготовление единицы продукции

Р₁ Р₂

S₁

S₂

S₃ -

S₄ -

Прибыль от реализации едины продукции (тыс. руб)

Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной

Последовательность действий по решению задачи:

1. Составление экономико-математической модели

2. Анализ полученной модели и выбор метода ее решения

3. Решение задачи выбранным методом

Графический метод обладает следующими достоинствами. Он достаточно прост и нагляден. Позволяет быстро получить искомый план. Однако у этого метода имеются существенные недостатки:

- невысокая точность вследствие погрешностей графических построений;

- рассмотренное (достаточно простое решение) может быть получено только, если целевая функция в стандартной задаче имеет всего две переменные.

1.2.2 Самостоятельное решение формализованной задачи (по номеру в журнале)

1) F = 2x₁ – 6x₂ → max 2) F = 2x₁ – x₂ → min