Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Практическая часть. Задание 2.2. 1Вычислить точки условного экстремума функции
|
|
Задание 2.2. 1 Вычислить точки условного экстремума функции
Z = x12 +х22,
при условии хl + х2 = 5.
Метод – коллективное решение задачи
Задание 2.2.2 Самостоятельное решение задачи (вариант по номеру в журнале)
Методом множителей Лагранжа определить условный экстремум функции.
Вариант 1 Z = x12 + x22, при условии х1 + х2 = 4:
Вариант 2 Z = x12 + x22, при условии х1 + х2 = 7;
Вариант 3 Z = x12 + x22, при условии х1 + х2 = 9;
Вариант 4 Z = x1х2 + x2х3, при ограничениях х1 + х2 = 2; х2 + х3 = 2;.
Вариант 5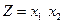 
при условии 
;
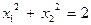Вариант 6 Z = x12 + x22 при условии x1 + x2 = 12;
Вариант 7 Z = x1 x2 + x2 x3, при условии x1 – x2 = 2; x2 + 2 x3 = 4
Вариант 8 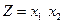при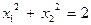
Вариант 9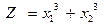 
, при условии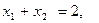 
Вариант 10 F = -x12 - x22при ограничении x1 + x2 = 1
Вариант 11 F = -x12 - x22при ограничении x1 + x2 = 2
Вариант 12 F = -x12 - x22при ограничении x1 + x2 =4
Вариант 13 F = x12 + x22при ограничении x1 + x2 = 9
Вариант 14 F = x12 + x22при ограничении x1+ x2 = 6
Вариант 15 F = x12 + x22при ограничении x1 + x2 = 8
Вариант 16 F = x12 + x22при ограничении x1+ x2 = 7
Вариант 17 F = x12 + x22при ограничении x1 + x2 = 10
Вариант 18 F = x12 + x22при ограничении x1+∙ x2 = 12
Вариант 19 F = x12 + x22при ограничении x1 + x2 = 13
Вариант 20 F = x12 + x22при ограничении x1 + x2 = 14
Вариант 21 F = 4x1 + x12 + 8x2 + x22 при условии x1 +x2 = 160
Вариант 22 F = x12 + x22 = x3 при условиях x1 + x2 + x3 = 4; 2x1 – 3x2 = 12
Вариант 23 F = x1 x2 x3 при условиях 2x1 x2 + x2x3 = 12; 2x1 – x2 = 8
Вариант 24 F = x1x2 + x2 x3 при условиях x1 + x2 = 4; x2 + x3 = 4
Вариант 25 F = 3x12 + 2x1 + 2x22 + 4x2x3 при условиях x12 + 2x22 = 19; x1 + 2x2 x3 = 11
Вариант 26 F = x1x2x3 при условиях x1 + x2 + x3 = 5; x1x2 + x2x3 + x1x3 = 8
Вариант 27 F = 2x1x2 +3 x2 x3 при условиях x1 + x2 = 6; x2 + x3 = 7
Вариант 28 F = 3x1x2 +2 x2 x3 при условиях 2x1 + x2 = 5; x2 + 3x3 = 6
Вариант 29 F = 4x1x2 +5x2 x3 при условиях 3x1 + x2 = 9; 2x2 + 3x3 = 10
Вариант 30 F = 7x1x2 +8x2 x3 при условиях 4x1 + x2 = 12; 5x2 + 2x3 = 14
Вариант 31 F = 9x1x2 +7x2 x3 при условиях 5x1 + x2 = 17; 3x2 + 6x3 = 19.
* * *