
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Краткие теоретические сведения. Если в задаче нелинейного программирования несколько (более двух ) переменных и имеются ограничения
|
|
Если в задаче нелинейного программирования несколько (более двух) переменных и имеются ограничения, заданные в форме равенств, то речь уже идет не о поиске безусловного, а условного оптимума. Такие задачи могут быть решены методом неопределенных множителей Лагранжа
Пусть задана задача математического программирования: максимизировать (минимизировать) функцию
Z = f (x1, x2, …, xn) (2.15)
при ограничениях
g(x1, x2, …, xn) = bi, 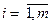 . (2.16)
. (2.16)
Ограничения в задаче заданы уравнениями, поэтому для ее решения можно воспользоваться классическим методом отыскания условного экстремума функции нескольких переменных.
Будем полагать, что функции z и gi являются непрерывными вместе со своими первыми производными.
Введем набор переменных λ 1, λ 2,...λ m, называемых множителями Лагранжа и составим функцию Лагранжа:
F(x1, x2, …xn, λ 1, λ 2,...λ m)=f(x1, x2, …xn) + 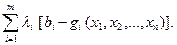 (2.17)
(2.17)
Определим частные производные:
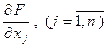 ;
;
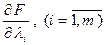
и рассмотрим систему (n + m) алгебраических уравнений
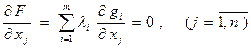
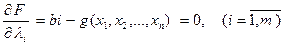 (2.18)
(2.18)
с (n + m) неизвестными x1, x2, …xn, λ 1, λ 2,...λ m.
Любое решение системы (8) определяет точку х = (x*1, x*2, …, x*n) в которой может иметь место экстремум функции f (x1, x2, …xn).
Следовательно, решив систему (4), можно получить все точки, в которых функция (5) может иметь экстремальные значения.
При этом неизвестен способ определения точек глобального минимума или максимума. Дальнейшее исследование полученных точек проводят так же, как и в случае безусловного экстремума, т.е. если для функции (1) существуют вторые частные производные и они непрерывны, то можно вывести достаточное условие существования локального экстремума функции в точке, являющейся решением системы (4). Однако практическое значение этого условия невелико.
Метод множителей Лагранжа имеет ограниченное применение, так как система уравнений (4), как правило, имеет несколько решений.