Виды линий положения.

В навигации чаще всего используются навигационные параметры, которые являются геометрическими величинами, то есть расстояниями, углами и пр. В этом случае каждому виду навигационного параметра соответствует своя геометрическая форма линии положения.

Рассмотрим те навигационные параметры и соответствующие им линии положения, которые в настоящее время применяются в навигации.

1. Навигационный параметр – горизонтальная дальность D. Под горизонтальной дальностью (далее будем называть ее просто дальностью) понимается кратчайшее расстояние от произвольной точки (места самолета) до некоторой фиксированной точки (радиомаяка) по поверхности Земли.

Этому параметру соответствует линия положения, называемая линией равных расстояний (ЛРР). На плоскости эта линия имеет форму окружности, в центре которой располагается радиомаяк. На земной сфере ЛРР также имеет вид окружности (малого круга), каждая точка которой одинаково удалена от радиомаяка. Расстояние, конечно, также измеряется по линии кратчайшего расстояния на сфере, то есть по дуге большого круга (ортодромии).

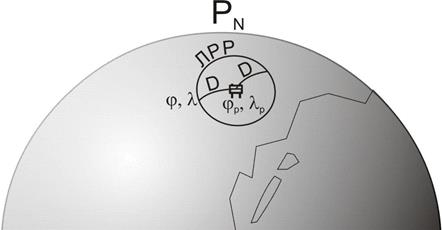
Рис. 2.13. Линия равных расстояний

Каждому численному значению дальности соответствует своя ЛРР. Все они являются окружностями с общим центром в точке расположения радиомаяка, образуя семейство ЛРР для данного радиомаяка

2. Навигационный параметр – пеленг самолета Пс. Напомним, что пеленг самолета – это угол, заключенный между северным направлением меридиана, проходящего через радиостанцию, и направлением на самолет. Параметру «пеленг самолета» соответствует линия положения, называемая линией равных пеленгов самолета (ЛРПС).

Когда мы говорим о направлении от радиостанции на самолет, мы имеем в виду, конечно, направление по линии кратчайшего расстояния, а не по какой-то извилистой кривой. На плоскости линией кратчайшего расстояния является прямая линия, а на сфере – это дуга большого круга. В какой бы точке этой линии ни находился самолет, пеленг на него от данной радиостанции будет один и тот же. Следовательно, ЛРПС имеет форму ортодромии (дуги большого круга), рис. 2.14.

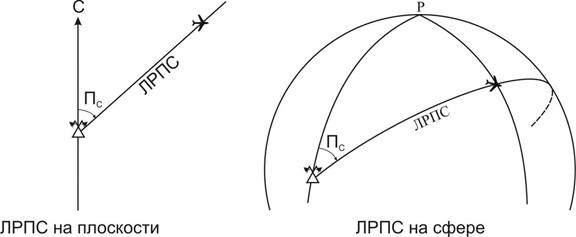
Рис. 2.14. Линия равных пеленгов самолета на плоскости и на сфере

Семейство ЛРПС, соответствующих разным значениям пеленга, представляет собой множество ортодромий, выходящих по всем возможным направлениям из точки расположения радиомаяка.

3. Навигационный параметр – пеленг радиостанции Пр. Пеленг радиостанции (радиомаяка) – это угол, заключенный между северным направлением меридиана, проходящего через самолет и направлением на радиомаяк. Линия положения, в каждой точке которой значение пеленга данной радиостанции является одинаковым, называется линией равных пеленгов радиостанции (ЛРПР).

Разумеется, и в этом случае имеется в виду направление на радиостанцию по кратчайшему расстоянию, то есть, на сфере – по ортодромии.

Принципиальная разница между двумя видами параметров и соответствующими линиями положения заключается в том, от какого именно меридиана отсчитывается параметр (пеленг). Пеленг самолета всегда отсчитывается от одного и того же меридиана – меридиана радиостанции, независимо от того в какой точке находится самолет. А пеленг радиостанции измеряется каждый раз от разных меридианов, а именно – от меридиана самолета.

Рассмотрим рис. 2.15. На нем линия ортодромического направления на радиостанцию от самолета обозначена пунктиром. В любой ее точке линия направления на радиостанцию совпадет с самой этой пунктирной линией. Но значение Пр в каждой точке будет разным, поскольку, как известно. ортодромия пересекает меридианы под разными углами. Следовательно, сама эта ортодромия не является ЛРПР, поскольку не обладает свойством сохранения постоянного значения параметра.

Но ЛРПР все же существует, однако проходит по-другому. А именно таким образом, чтобы в каждой ее точке угол (Пр) между меридианом этой точки и ортодромическим направлением от нее на радиостанцию был одинаков (см. рис. 2.15).

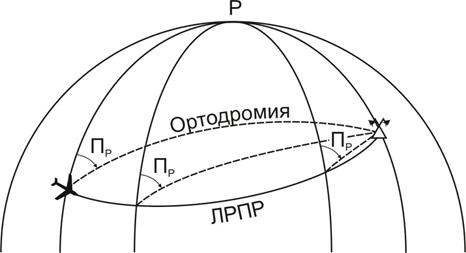
Рис. 2.15. Линия равных пеленгов радиостанции

ЛРПР на сфере имеет сложную форму, которая называется сферической лемнискатой Бернулли.

Различие между ЛРПР и ЛРПС объясняется наличием угла схождения меридианов δ сх радиостанции и самолета. Чем он меньше, тем ближе друг к другу проходят ЛРПР и ортодромическая ЛРПС.

4. Навигационный параметр – разность расстояний от самолета до двух радиостанций. Этому параметру соответствует линия положения, называемая линией равных разностей расстояний (ЛРРР).

Пусть самолет (рис. 2.16) находится в некоторой точке, расстояния от которой до двух известных радиостанций составляют соответственно D1 и D2. Допустим, что сами эти дальности на борту не измеряются, но в любой момент времени может быть измерена их разность.

Технически измерить разность расстояний не измеряя самих расстояний вполне возможно, причем даже несколькими способами. Как именно это делается будет рассмотрено в главе о разностно-дальномерных системах.

Поскольку сами дальности являются навигационными параметрами, то есть их значения зависят от места самолета, то и их разность Δ D также является навигационным параметром. Линия положения для этого параметра (ЛРРР) имеет форму гиперболы. Из математики известно, что гипербола обладает следующим свойством: разность расстояний от любой точки гиперболы до двух фиксированных точек, называемых фокусами гиперболы, является постоянной. В нашем случае этими фокусами и являются две радиостанции. Попутно заметим, что похожим свойством обладает и другая кривая второго порядка – эллипс, для каждой точки которого сумма расстояний до двух фокусов эллипса одинакова.

На плоскости ЛРРР является обычной гиперболой, ветви которой уходят в бесконечность, а на земной сфере – сферической гиперболой, которая является замкнутой кривой (рис. 2.17).

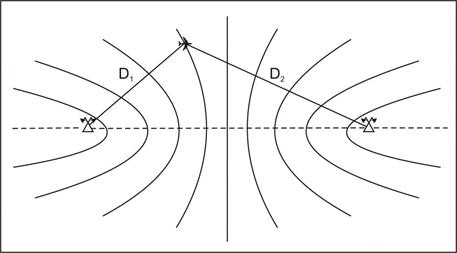
Рис. 2.16. Линии равных разностей расстояний на плоскости

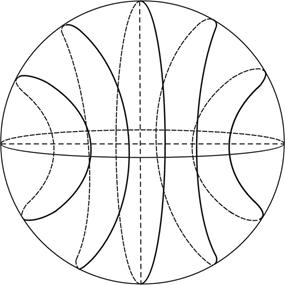
Рис. 2.17. Линии равных разностей расстояний на сфере

Каждому значению параметра Δ D соответствует своя гипербола, а все множество этих гипербол составляет семейство этих линий положения. Каждая гипербола является симметричной относительно линии базы, то есть прямой, проходящей через обе радиостанции. Чем больше Δ D по абсолютной величине, тем круче изогнута гипербола (наибольшая крутизна имеет место вблизи линии базы). И наоборот, чем меньше Δ D, тем больше распрямляются ветви гиперболы. В частном случае, когда Δ D=0, то есть расстояния до обеих радиостанций одинаковы, гипербола, если рассматривать ее на плоскости, превращается в прямую, проходящую через середину линии базы перпендикулярно к ней. При дальнейшем уменьшении Δ D (параметр будет уже отрицательным) ветви ЛРРР загибаются уже в противоположную сторону. Семейство ЛРРР расположено симметрично относительно перпендикуляра к середине базы.

Теоретически можно рассмотреть линии положения, соответствующие и любым другим навигационным параметрам. Например, в качестве параметров можно рассматривать сумму расстояний до двух радиостанций, разность пеленгов двух радиостанций и т.п. Каждому из них будет соответствовать линия положения определенной формы.