Виды погрешностей. Средняя квадратическая погрешность.

Виды погрешностей. Практически всегда погрешность включает в себя две составляющие ее части: систематическую и случайную.

Δ a= Δ aсист + Δ aслуч.

Систематической называется погрешность, которая в данных условиях сохраняет постоянное значение (или изменяется, но по известному закону).

Такие погрешности вызваны постоянно действующими причинами, в результате чего при измерении мы каждый раз «ошибаемся» на одну и ту же величину. Очень часто такие погрешности вызваны неточным изготовлением прибора (инструментальные погрешности), или постоянным внешним фактором. Например, собственное магнитное поле самолета вызывает погрешность измерения магнитного курса (девиацию), которая на каждом курсе имеет вполне определенное значение.

Систематические погрешности, поскольку они одинаковы при каждом измерении, можно один раз определить с помощью более точных приборов, а затем исключать их из результатов измерений путем ввода поправок.

Систематические погрешности не доставляют особых хлопот при навигации, поскольку после их устранения они уже отсутствуют. Поэтому далее будем считать, что систематические погрешности отсутствуют (уже учтены).

Случайная погрешность при каждом измерении принимает разное значение, причем заранее неизвестно какое именно.

А вот случайные погрешности в принципе устранить нельзя, поскольку они при каждом измерении различны. И они всегда остаются неизвестными.

Определить численные значения случайных погрешностей невозможно, однако пилот постоянно должен иметь в виду, что эти погрешности существуют и иметь представление об их возможных значениях. Наличие неопределенности в результатах измерений является одним из основных факторов, усложняющих навигацию и делающих ее не только наукой, и искусством.

Случайным событием называют событие, которое при данных условиях может произойти или не произойти. Степень возможности наступления такого события численно характеризуют величиной вероятности. Вероятность Р – это число, которое может лежать в пределах от 0 до 1. Если при данных условиях событие никогда не происходит, его называют невозможным событием и его вероятность равна нулю. Если же оно при данных условиях происходит всегда, то его называют достоверным и приписывают ему вероятность равную единице. Если, например, Р=0, 3, то это означает, что в среднем в 30 случаях из 100 событие произойдет. Именно в среднем, поскольку событие является случайным. Если создать необходимые для наступления события условия и провести серию из 100 опытов, то событие может произойти, например, 23 раза, или 32 раза… Если провести несколько серий таких опытов, или одну серию из тысячи, десяти тысяч, миллиона опытов, то, чем большее количество опытов проведено, тем ближе среднее количество наступлений события будет ближе к 30% от общего количества опытов (если Р=0, 3).

Каким же образом можно описать случайные погрешности, если они не имеют какого-либо определенного значения? Часто их характеризуют величиной средней квадратической погрешности (СКП), которая обозначается буквой σ (сигма). Так, например, СКП измерения величины a будем обозначать σ a.

СКП является характеристикой степени рассеяния измеренного значения величины вокруг фактического ее значения. Чем больше σ a, тем больше рассеяны (разбросаны) измеренные в разных опытах значения вокруг фактического значения величины.

На рис. 2.19 геометрически представлены в виде числовой оси возможные значения измеряемой величины a и отмечено фактическое ее значение. Крестиками на шкале обозначены полученные в результате нескольких опытов измеренные значения. В первом случае разброс измеренных значений вокруг фактического больше, чем во втором случае, следовательно «сигма», которая и характеризует степень разброса, во втором случае меньше.

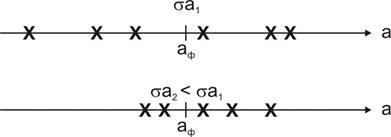
Рис. 2.19. Средняя квадратическая погрешность

По величине СКП можно судить о вероятностях того, что измеренное значение примет то или иное значение. Но для этого недостаточно знать СКП, нужно также знать, какому закону распределения подчиняется данная случайная погрешность. Многие случайные величины подчиняются нормальному (гауссовскому) закону распределения. Для этого закона полезно запомнить следующие значения.

Если систематическая погрешность отсутствует и в результате измерения получено значение aизм, то фактическое значение величины лежит в пределах (рис. 2.20):

aизм ± σ a с вероятностью Р=0, 68;

aизм ± 2σ a с вероятностью Р=0, 95;

aизм ± 3σ a с вероятностью Р=0, 997.

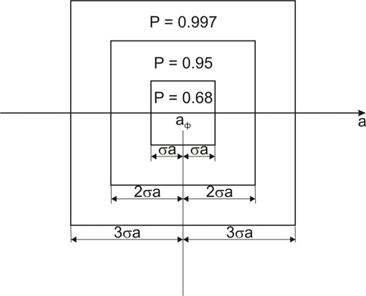
Рис. 2.20. Некоторые вероятности для нормального закона распределения

Например, с помощью компаса измерен курс γ =100º, а точность компаса характеризуется СКП σ γ =2º. Это означает, что фактический курс (который так и останется нам неизвестным) в среднем:

в 68 случаях из 100 лежит в пределах 100º ±2º, то есть в интервале 98º …102 º;

в 95 случаях из 100 лежит в пределах 100º ±4º, то есть в интервале 96º …104º;

в 997 случаях из 1000 лежит в пределах 100º ±6º, то есть в интервале 94º …106º.

Значение вероятности Р =0, 997 настолько близко к единице, что соответствующее ей значение погрешности в «три сигмы» часто называют максимальной погрешностью. На самом деле погрешность может его и превысить. Правда, редко – в среднем в трех случаях из тысячи.

В технических описаниях приборов и оборудования их точность может быть указана непосредственно в виде СКП и тогда все понятно. Но иногда ее указывают, например, так: «погрешность измерения пеленга ±1, 5º». Разумеется, это не означает, что такой пеленгатор «ошибается» каждый раз на 1, 5º. Это также не означает, что он не может ошибиться более, чем на 1, 5º. Как правило, указанное таким образом значение погрешности соответствует вероятности Р =0, 95. То есть в среднем в 95 случаях из 100 погрешность не превысит (в большую или меньшую сторону) значения в 1, 5º.

Соответственно, в пяти случаях из ста погрешность может быть и больше. Для нормального закона распределения погрешности вероятность 0, 95 соответствует удвоенной СКП. Следовательно, СКП измерения пеленга в данном примере составит 0, 75º.