Розв’язування транспортної задачі

Розв’язування транспортної задачі відбувається за допомогою так званої транспортної таблиці, загальний вигляд якої подано у табл. 8.1. У клітинках з індексами i, j таблиці записано величини 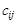(у верхньому правому куті); у процесі розв’язування в деяких клітинах з’являться ненульові 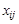, а також додаткова інформація.

Таблиця 1.1

Пункти відправлень	Пункти призначення	Запаси
		...		…
			...		…
			…		…
…	…	…	…	...	…	...	...
			…	,	…
…	...	…	…	…	…	...	…
			…		…
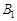
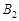
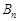
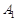
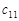
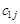
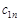
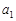
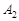
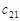
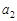
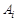
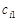
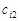
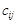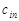
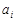
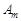
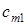
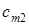
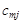
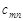
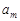
Заявки			…		…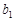

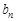
Рядки таблиці відповідають умовам (1.3), стовпчики – умовам (8.2).

Розв’язування ТЗ пояснимо на прикладі конкретної задачі, наведеної в табл. 1.2. Тут , .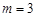

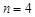Приклад 1.1. Розв’язати ТЗ, умова якої задана в таблиці 1.2.

Таблиця 1.2

Пункти відправлень	Пункти призначення	Запаси
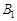
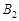
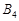
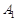
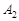
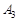
Заявки

Розв’язування ТЗ містить два етапи:

- побудова опорного плану;

- побудова оптимального плану.

Побудова опорного (базисного) плану.

Існує кілька ефективних методів знаходження допустимого і одночасно базисного (опорного) плану. Наведемо найпростіший з них, так званий метод північно-західного кута (назва походить від положення початкової лівої верхньої клітинки).

Розглянемо заявку з індексом 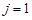, що становить 10 одиниць, і запас з індексом 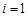, що становить 25 од. Візьмемо меншу з цих величин і покладемо 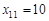. Заявка задоволена, залишається запас у 15 од., що піде на задоволення заявки 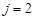. Покладемо . Заявка і запас вичерпані. Звернемося до клітинки (2; 3): заявка 45 од., запас 35 од. Покладемо 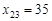, дал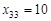і і . Усі заявки забезпечені, запаси вичерпані. Підрахуємо кількість ненульових перевезень, яких намічується п’ять, а повинно бути 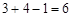. Щоб забезпечити потрібну кількість базисних клітин, треба у випадку, коли одночасно вичерпуються заявка і запас (так званий випадок виродженості), включити в базис ще одну (сусідню справа або знизу) клітину, записавши в неї величину або 0. Таким чином маємо табл. 1.3, де збалансовані заявки і запаси і є необхідна кількість базисних змінних, тобто 6.

Таблиця 1.3

Сформулюємо алгоритм методу північно-західного кута.

1. Беремо верхню ліву клітинку таблиці.

2. Порівнюємо заявку і запас. Менше з цих значень записуємо у клітинку. Від заявки і запасу віднімаємо цю величину. Переходимо до п. 3.

3. Якщо заявка була більша від запасу, беремо наступну знизу клітинку і переходимо до п. 2, інакше до п. 4.

4. Якщо запас був більше, ніж заявка, беремо наступну справа клітинку і переходимо до п. 2, інакше – до п. 5.

5. Запас і заявка рівні. Записуємо значення в клітинку, віднімаємо від заявки і запасу. Визначаємо, чи була клітина останньою (правою нижньою). Якщо так – переходимо до п. 7, якщо інакше – на п. 6.

6. У сусідню клітинку справа записуємо 0 і вважаємо її базисною. Беремо сусідню клітинку знизу і переходимо до п. 2.

7. Кінець.

На відміну від симплекс-таблиці, у транспортній таблиці цільова функція не наведена і автоматично не підраховується. Знайдемо її початкове значення 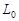для табл. 1.3.

.

Лекція 2. Знаходження оптимальногоплану перевезень методом потенціалів

2.1. Цикли як засоби поліпшення плану перевезень

Базисний план, наведений у табл. 8.3, очевидно, не оптимальний (зайняті клітини з великою вартістю і вільні з малою). Спробуємо зайняти клітину (2; 2), перенісши туди перевезення об’ємом 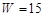з клітини (1; 2). Щоб зберігся баланс, треба від клітини (2; 3) відняти величину , а до клітини (1; 3) додати величину та отримати табл. 2.1.

Таблиця 2.1

Підрахуємо нове значення цільової функції:

,

тобто цільова функція зменшилася на 120 од.

Дія, яку ми виконали, називається перенесенням по циклу. Такі операції і є інструментом поліпшення плану перевезень у ТЗ, що в результаті приведе до формування оптимального плану. Наведемо теоретичні і технічні відомості про ці операції.

Означення. Циклом у транспортній таблиці називається замкнена ламана лінія з вершинами у клітинах і ланками по рядках і стовпчиках, яка задовольняє умови:

- у кожній вершині зустрічаються дві ланки, одна розміщена по рядку, друга – по стовпчику;

- у кожній вершині здійснюється поворот на 90^о.

З означення циклу випливають його властивості:

- ніякі три сусідніх вершини не можуть знаходитися в одному рядку чи стовпчику;

- циклом може служити ламана, що самоперетинається, але точки перетину не можуть служити вершинами циклу.

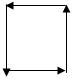
Було здійснено простий цикл, що охоплював чотири клітини (табл. 2.2).

Таблиця 2.2

-	+
+	-

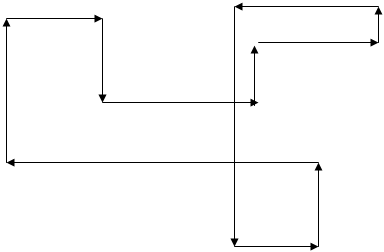
Цикли можуть бути набагато складнішими (табл. 2.3), де вершини циклу позначені хрестиками.

Таблиця 2.3

х		х		х			х
					х		х
		х			х
х						х
				х		х

Означення. Нехай є цикл, в якому деяка вершина вибрана як початкова. Надамо їй знак „+”, наступній „-” і т.д. Такий цикл називаємо означеним; клітини зі знаком „+” – додатними, із знаком „-” – від’ємними. Очевидно, у кожному рядку і стовпчику кількість додатних і від’ємних клітин буде рівною.

Цикл у табл. 2.2. зробили означеним.

Означення. Перенесенням по циклу називається таке переміщення величини перевезень 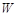, при якому величина 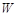додається до всіх додатних клітин і віднімається від усіх від’ємних. Величина 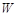дорівнює найменшій з величин 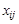у від’ємних клітинах.

Таким чином, перейшовши від табл. 1.3 до табл. 1.4, здійснили перенесення по циклу, наведеному у табл. 2.2.

Означення. Розглянемо будь-яку вільну клітину. Циклом перерахунку для цієї клітини називається означений цикл, в якому ця клітина є додатною вершиною, а всі інші клітини належать базисним клітинам.

У результаті циклу перерахунку ця вільна клітина стає базисною, а одна з базисних вільною.

Примітка. Якщо у циклі перерахунку величина 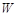з’являється одночасно у кількох від’ємних клітинах, до числа вільних переходить лише одна з них, у решту записуємо нуль і вважаємо, як і раніше, базисними. Це необхідно для збереження потрібної кількості базисних клітин. Таким чином, план залишається допустимим і базисним. Цикл перерахунку є єдиним і ефективним засобом поліпшення плану перевезень.

Проаналізуємо доцільність операції перенесення по циклу.

Означення. Ціною циклу називається величина, на яку змінюється функція , якщо перенести по циклу одиницю вантажу.

У прикладі 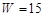, , тому

.

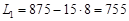Видно, що після здійснення циклу перерахунку немає необхідності робити повний розрахунок функції 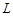; досить застосувати її коригування за формулою (2.2).

Ознака оптимальності плану. План перетворень є оптимальним, якщо не існує вільних клітин з від’ємного ціною циклу.

Існує кілька методів поліпшення плану перевезень. Згідно з одним з них, так званим розподільчим, після кожного перерахунку перебираються вільні клітини; для кожної будується цикл, за формулою (9.2) визначається його ціна і доцільність перенесення. Цей процес надто трудомісткий.

Виникає питання: чи не можна визначити ціну циклу, не будуючи його? Це виявилося здійсненним, коли був розроблений так званий метод потенціалів.