
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Касательная плоскость и нормаль к поверхности.
|
|
1. Уравнение касательной плоскости и нормали для случая явного задания поверхности.
Определение. Касательной плоскостью к поверхности 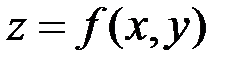 в точке
в точке 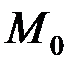 (точка касания) называется плоскость, в которой лежат все касательные в точке
(точка касания) называется плоскость, в которой лежат все касательные в точке 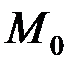 к различным кривым, проведенным на поверхности через эту точку.
к различным кривым, проведенным на поверхности через эту точку.
Определение. Нормалью к поверхности называется перпендикуляр к касательной плоскости в точке касания.
Если 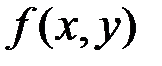 – дифференцируемая функция, то уравнение касательной плоскости в точке
– дифференцируемая функция, то уравнение касательной плоскости в точке 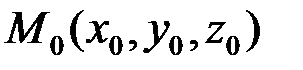 поверхности имеет вид
поверхности имеет вид
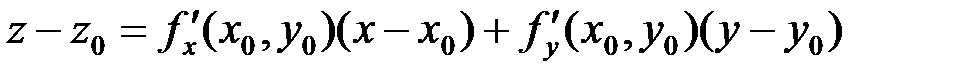 (5)
(5)
Уравнения нормали имеют вид
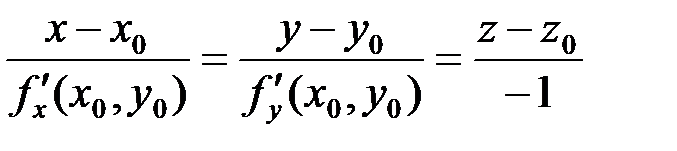 . (6)
. (6)
Пример 2. Найти уравнения касательной плоскости и нормали к поверхности 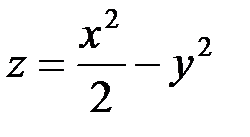 в точке
в точке 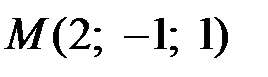 .
.
2. Уравнение касательной плоскости и нормали для случая неявного задания поверхности.
Пусть уравнение гладкой поверхности задано в неявной форме 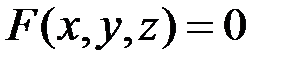 и
и 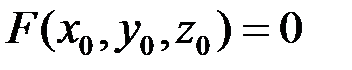 . Тогда соответствующие уравнения будут иметь такой вид:
. Тогда соответствующие уравнения будут иметь такой вид:
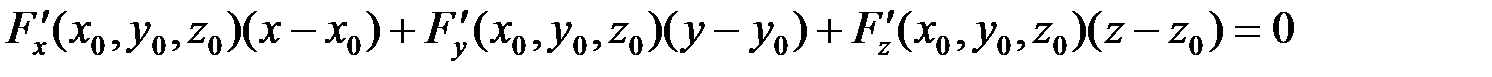
– уравнение касательной плоскости и
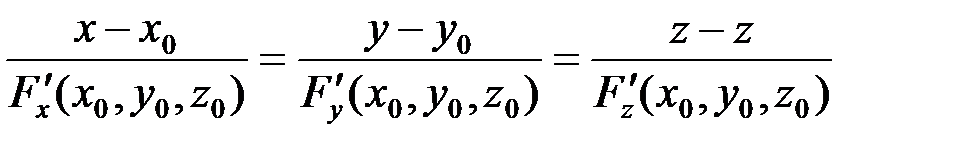 .
.
– уравнение нормали к поверхности.
Пример 3. Написать уравнение касательной плоскости и нормали к поверхности 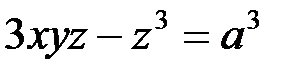 в точке, для которой
в точке, для которой 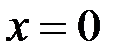 ,
, 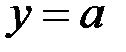 .
.
Решение. Найдем аппликату точки касания, подставив 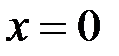 и
и 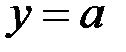 в уравнение поверхности:
в уравнение поверхности:  . Таким образом, точка касания
. Таким образом, точка касания 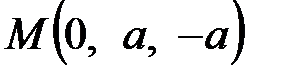 .
.