Замена независимых переменных в выражении, содержащем частные производные.

Если в дифференциальном выражении

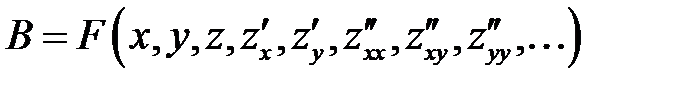
положить 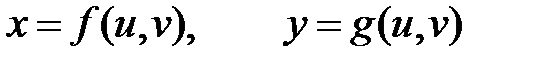, (8)

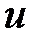где и 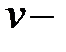новые независимые переменные, то частные производные 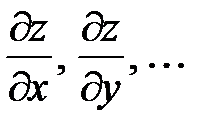определяются из следующих уравнений:

, .

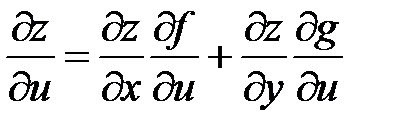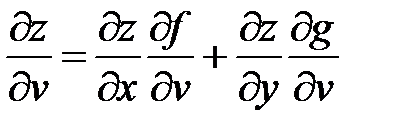Пример 6. Уравнение колебаний струны 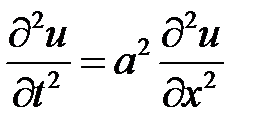преобразовать к новым независимым переменным 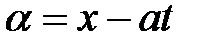и .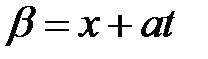

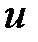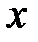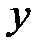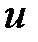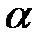Решение. Выразим частные производные от по и через частные производные от по и .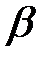

Очевидно,

,

.

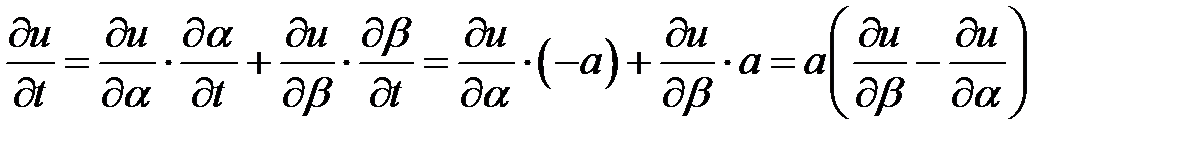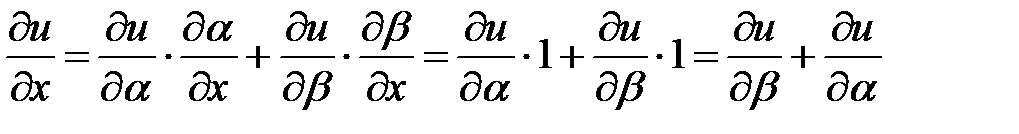Дифференцируем вторично, применяя ту же формулу

,

.

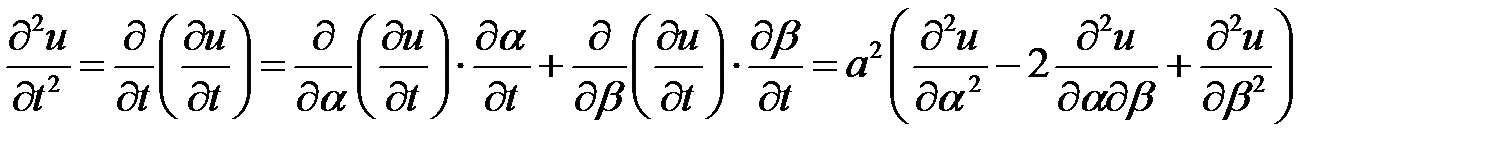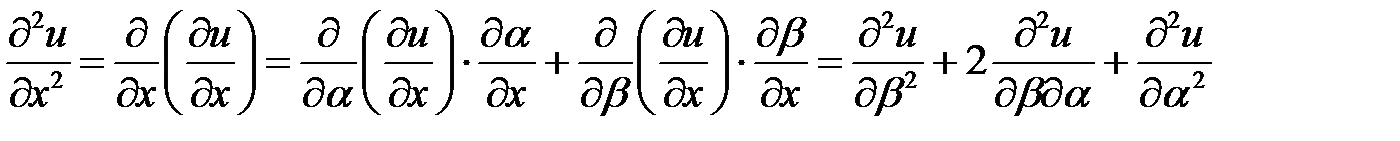Подставив в уравнение, получим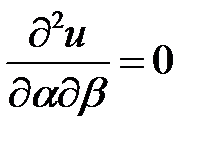

Пример 7. Преобразовать уравнение 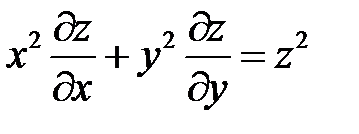, приняв за новые независимые переменные 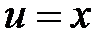, 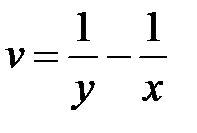и за новую функцию .

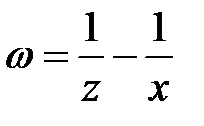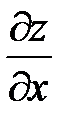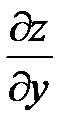Решение. Выразим частные производные и через частные производные 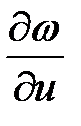и 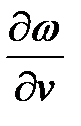. Для этого продифференцируем данные соотношения между старыми и новыми переменными:

.

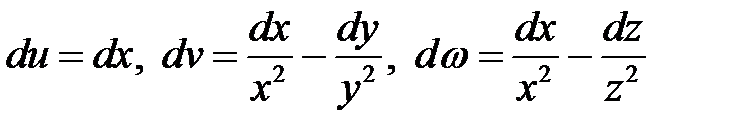С другой стороны,

.

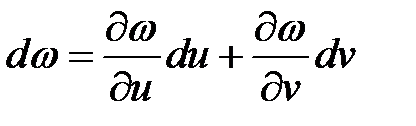Поэтому

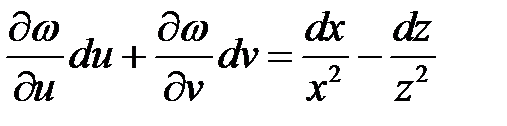
или

.

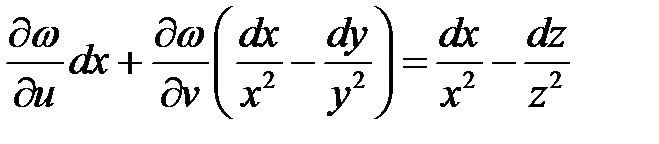Отсюда

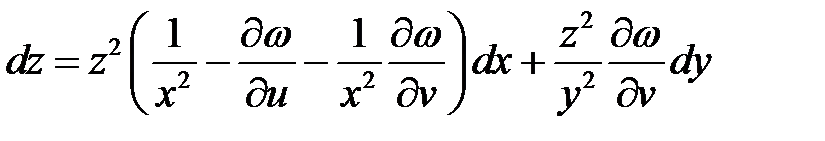
и, следовательно,

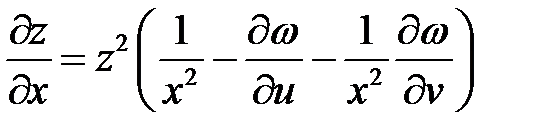и .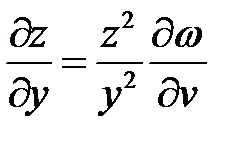

Подставляя эти выражения в данное уравнение, получим

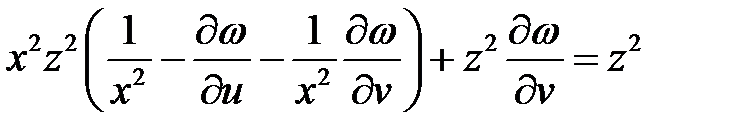или 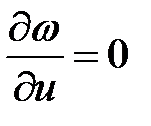.