
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие функционала
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Казанский национальный исследовательский технический университет им. А.Н.Туполева-КАИ»
(КНИТУ-КАИ)
Г.Л.Дегтярёв
Оптимальное управление
(Учебное пособие)
Казань 2014
Теория оптимального управления
Литература
1. Эльсгольц «Вариационное исчисление».
2. Сиразетдинов Т.К. «Оптимизационные задачи авиационной техники».
3. Сиразетдинов Т.К. «Основы теории оптимальных процессов».
4. Дегтярев Г.Л., Семенов П.К. «Оптимальное управление стохастическими системами при неполной информации».
5. Брайсон, Хо-Ю-ШИ «Прикладная теория оптимального управления».
6. Дегтярев Г.Л., Ризаев И.С. «Синтез локально-оптимальных алгоритмов управления ЛА».
7. Ройтенберг Я.И. Автоматическое управление.
1. Математическая постановка задач оптимального управления.
Предположим, что управляемый процесс описывается совокупностью дифференциальных уравнений
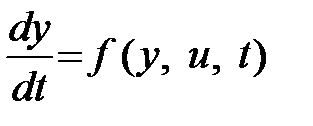 (1.1)
(1.1)
с начальными условиями
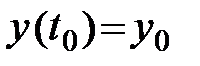 (1.2)
(1.2)
Здесь:  - n - мерная функция своих аргументов,
- n - мерная функция своих аргументов,
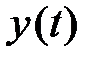 - n - мерный вектор, характеризующий состояние управляемого процесса в момент времени
- n - мерный вектор, характеризующий состояние управляемого процесса в момент времени 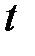 ,
,
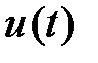 - r - мерный вектор управляющих воздействий (из некоторого заданного класса функций),
- r - мерный вектор управляющих воздействий (из некоторого заданного класса функций), 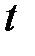 - время,
- время,
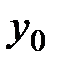 - начальное состояние.
- начальное состояние.
Если управление 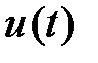 на отрезке
на отрезке  , где
, где 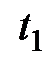 - конечное время управления, задано
- конечное время управления, задано 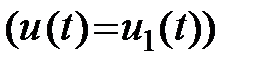 , можно построить соответствующее ему решение системы (1.1), (1.2)
, можно построить соответствующее ему решение системы (1.1), (1.2) 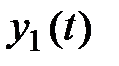 .
.

| t 0 |
| t 1 |
| t 0 |
| t 1 |
| y 2(t) |
| y 1(t) |
| u 1(t) |
| u 2(t) |
| u (t) |
| y (t) |
| Рис. 1 |
Другому управлению
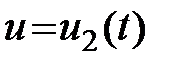 будет соответствовать другая траектория
будет соответствовать другая траектория 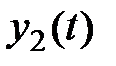 .
.
Как известно, задача синтеза управления заключается в построении таких управляющих воздействий, при которых выполняется совокупность ограничений на состояние процесса, например, по времени переходного процесса, по величине максимального перерегулирования и т.п.
Задача же оптимального управления заключается в отыскании таких управляющих воздействий, при которых управляемый процесс будет наилучшим в некотором смысле. При этом для оценки качества управляемого движения вводится функционал 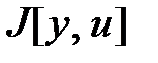 .
.
Понятие функционала
Известно, что если каждому значению переменной 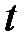 соответствует определенное значение переменной
соответствует определенное значение переменной 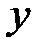 , то говорят, что задана функция
, то говорят, что задана функция 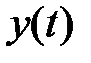 .
.
Если каждой функции 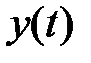 можно поставить в соответствие некоторое числовое значение переменной
можно поставить в соответствие некоторое числовое значение переменной  , то говорят, что задан функционал
, то говорят, что задан функционал 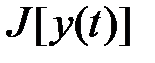 на множестве реализаций функции
на множестве реализаций функции 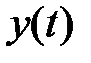 . Таким образом, областью определения функционала является множество функций.
. Таким образом, областью определения функционала является множество функций.
Примерами функционала может быть длина  кривой
кривой 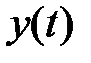 , соединяющей две точки
, соединяющей две точки 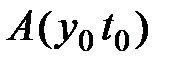 и
и 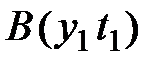 на плоскости
на плоскости

| t 0 |
| t 1 |
| y 0 |
| y 1 |
| y |
| A(y 0 t 0) |
| B(y 1 t 1) |
| Рис. 2 |
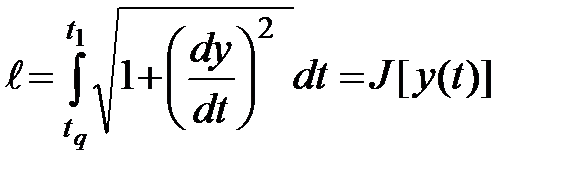 ,
,
или площадь 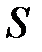 , ограниченная кривой
, ограниченная кривой 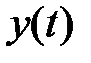
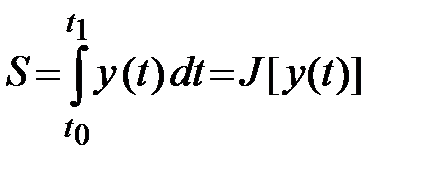 .
.
В качестве функционала может быть расход топлива, необходимый для перелета самолета из пункта  в пункт
в пункт  . Величина этого расхода будет зависеть от выбранной траектории полета.
. Величина этого расхода будет зависеть от выбранной траектории полета.
В качестве функционала может рассматриваться значение функции в некоторой точке 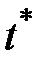 , т.е.
, т.е.
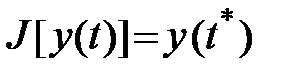 .
.
В качестве такой точки 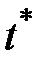 может быть конечная точка
может быть конечная точка 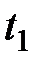 , т.е.
, т.е. 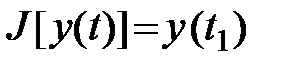 или некоторая функция
или некоторая функция  конечного состояния, т.е.
конечного состояния, т.е.
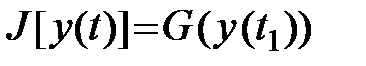 .
.
Различают следующие виды функционалов.
1) Функционал Лагранжа
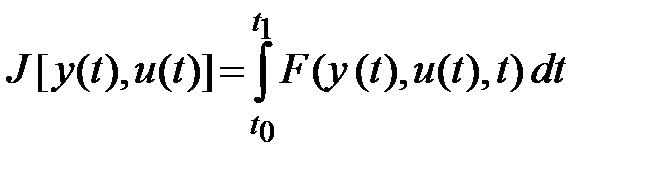 , (1.3)
, (1.3)
где 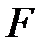 - некоторая достаточно-гладкая функция своих аргументов, свойства которой оговариваются в конкретном случае.
- некоторая достаточно-гладкая функция своих аргументов, свойства которой оговариваются в конкретном случае.
2) Функционал Майера
 (1.4)
(1.4)
3) Функционал Больца
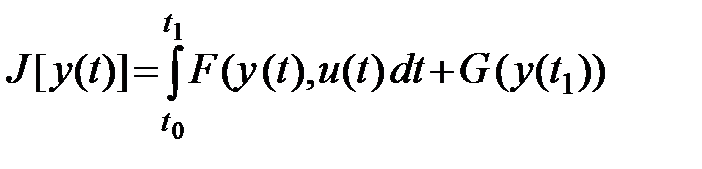 (1.5)
(1.5)
В смысловом плане эти функционалы различаются, но с точки зрения математической принципиальной разницы нет, т.к. от одной формы представления функционала можно перейти к другой.
Например, путем введения переменной
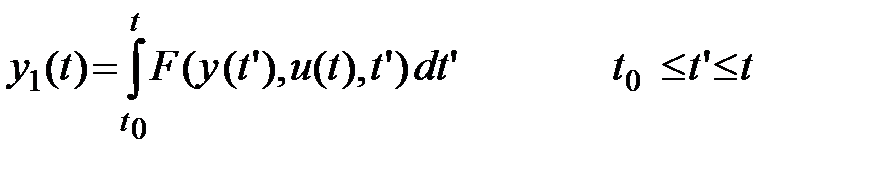
функционал Лагранжа
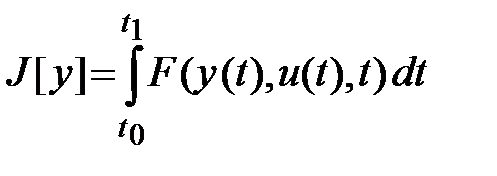
можно представить в форме Майера
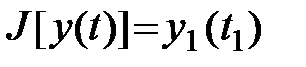 ,
,
где 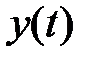 и
и 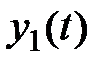 связаны уравнением
связаны уравнением
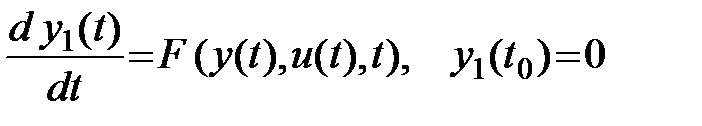 .
.
4) Локальный функционал. Рассмотренные функционалы характеризуют качество управляемого процесса на конечном (или бесконечном) интервале времени. Однако часто бывает необходимо, чтобы поведение системы было оптимальным в некотором смысле в любой текущий момент времени. К таким требованиям относится, например, требование максимальной текущей точности функционирования системы. В этом случае критерием оптимальности служит некоторый функционал (функция) 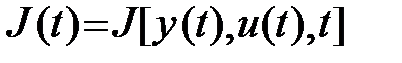 , параметрически зависящий от времени
, параметрически зависящий от времени 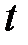 , определенный на множестве функций
, определенный на множестве функций 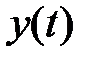 и
и 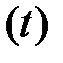 . Общий вид такого функционала можно представить в следующем виде
. Общий вид такого функционала можно представить в следующем виде
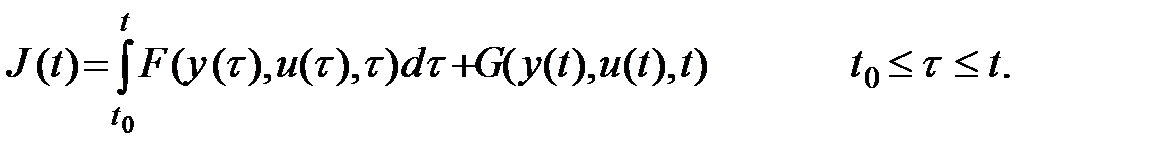 (1.6)
(1.6)
Управление 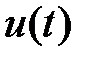 , минимизирующее
, минимизирующее 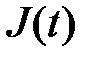 в текущий момент времени, называется локально-оптимальным.
в текущий момент времени, называется локально-оптимальным.
Теперь задача оптимального управления может быть сформулирована как задача поиска такой управляющей функции 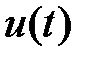 и соответствующей траектории
и соответствующей траектории 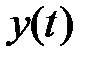 , удовлетворяющей системе (1.1), (1.2), на которых некоторый функционал
, удовлетворяющей системе (1.1), (1.2), на которых некоторый функционал 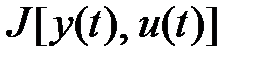 достигает минимального или максимального значения.
достигает минимального или максимального значения.
При этом каждый раз оговаривается класс функций, среди которых отыскивается минимум или максимум (класс функций сравнения).
Это может быть класс непрерывных, кусочно-непрерывных или непрерывно-дифференцируемых определенное число раз функций. Свойства любого функционала существенно зависят от того, на каком классе функций он задан.
В том случае, когда функция 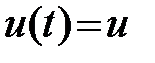 - не зависит от времени (постоянна), функционал становится функцией этого параметра и задача оптимизации сводится к задаче минимизации (максимизации) функции.
- не зависит от времени (постоянна), функционал становится функцией этого параметра и задача оптимизации сводится к задаче минимизации (максимизации) функции.

| v (p) |
| u (p) |
| W (p) |
| y (p) |
| Рис. 3 |
Рассмотрим систему, где
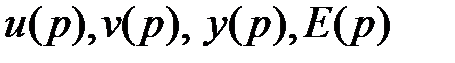 - изображения
- изображения
(по Лапласу) задающего воздействия  , помехи
, помехи 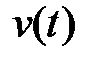 , выходной переменной
, выходной переменной 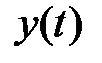 и ошибки системы
и ошибки системы 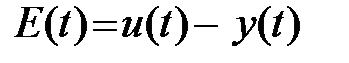 , соответственно,
, соответственно,
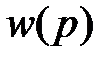 - передаточная функция разомкнутой системы.
- передаточная функция разомкнутой системы.
Учитывая, что 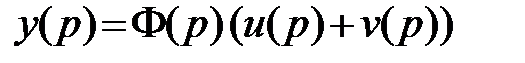 , где
, где 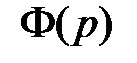 - передаточная функция замкнутой системы, получим
- передаточная функция замкнутой системы, получим
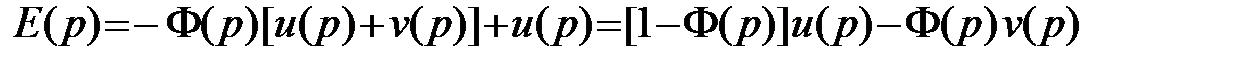 .
.
Предположим, что 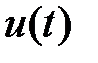 и
и 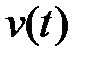 - независимые стационарные случайные процессы с известными спектральными плотностями (плотностями распределения дисперсии по частотам)
- независимые стационарные случайные процессы с известными спектральными плотностями (плотностями распределения дисперсии по частотам) 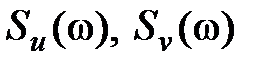 . Тогда спектральная плотность ошибки системы
. Тогда спектральная плотность ошибки системы
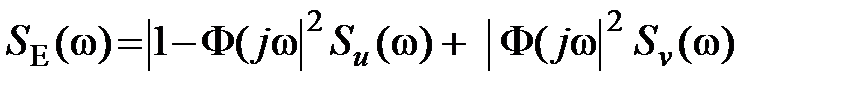 , где
, где 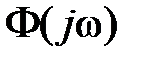 - частотная функция замкнутой системы.
- частотная функция замкнутой системы.

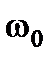
|

|
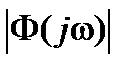
|
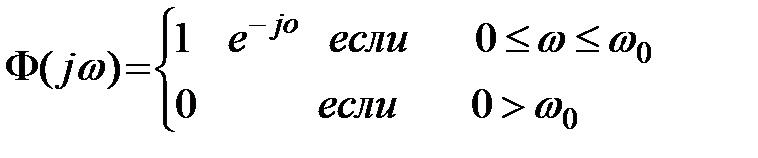 ,
,
т.е. АЧХ системы  .
.
Здесь 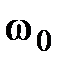 - характеризует ширину полосы пропускания системы.
- характеризует ширину полосы пропускания системы.
Тогда дисперсия ошибки
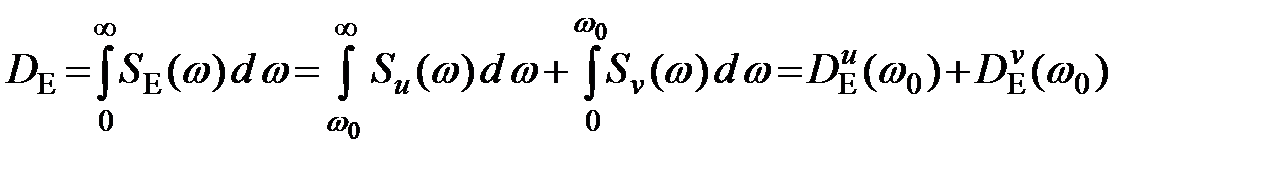
при заданных 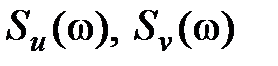 является функцией
является функцией 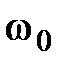 , причем, с увеличением
, причем, с увеличением 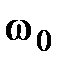
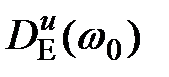 уменьшается, а
уменьшается, а 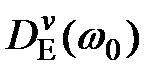 увеличивается, т.е. с увеличением
увеличивается, т.е. с увеличением 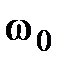 лучше отрабатывается полезный сигнал, но увеличивается влияние помехи. Поэтому может быть поставлена задача определения такой
лучше отрабатывается полезный сигнал, но увеличивается влияние помехи. Поэтому может быть поставлена задача определения такой 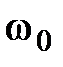 , при которой дисперсия ошибки является минимальной. Используя необходимые условия экстремума
, при которой дисперсия ошибки является минимальной. Используя необходимые условия экстремума
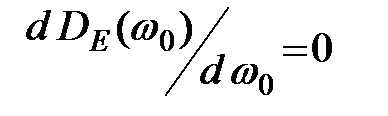 ,
,
получим уравнение, которому с необходимостью удовлетворяет искомая оптимальная ширина полосы пропускания системы 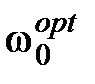
 . (1.7)
. (1.7)

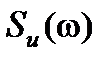
|
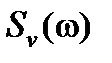
|
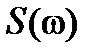
|

|
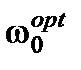
|
| Рис. 4 |
Так как уравнение (1.7) – нелинейное, оно может иметь несколько решений, каждое из которых должно быть дополнительно исследовано и найдено действительно оптимальное.
Методы решения задач оптимального управления
Теоретической основой решения задач оптимального управления являются:
1) вариационное исчисление,
2) принцип максимума Понтрягина,
3) метод динамического программирования Беллмана.
В том случае, когда задача оптимального управления сводится к параметрической оптимизации для поиска оптимальных параметров, используются методы минимизации функций.