Дисперсия это средний квадрат отклонений от индивидуальных значений признака от их средней величины.

Лекция №3 (4часа)

Показатели вариации

Средняя величина дает обобщающую характеристику всей совокупности изучаемого явления. Однако два ряда распределения, имеющие одинаковую среднюю арифметическую величину, могут значительно отличаться друг от друга по степени колеблемости (вариации) величины изучаемого признака. Наличие различий в величине признака у отдельных единиц совокупности обусловлено влиянием большого числа факторов. Эти факторы могут оказывать разнонаправленное воздействие на анализируемый показатель. Например, снижение цен на строительные материалы может привести к уменьшению цен на I м² жилья, а увеличение спроса на жилье может повысить эту цену и т.д. В результате совместного влияния различных факторов и складывается цена I жилья в определенное время. Но есть, например, и такой фактор, как экологическая обстановка в разных районах или географическое положение района, которая также обусловливает вариацию цен 1 м² жилья в разных районах города. Поэтому при изучении вариации показателей можно выделить две группы факторов, влияющих на уровень и вариацию признака в исследуемой совокупности. Первую - составляют факторы, общие для всех единиц изучаемой совокупности. Во вторую группу входят факторы, свойственные конкретным единицам совокупности и определяющие их индивидуальные особенности. Если индивидуальные значения признака ряда мало отличаются друг от друга, то средняя арифметическая будет достаточно показательной характеристикой свойств данной совокупности. Если значения признака характеризуются значительным рассеянием, то средняя арифметическая будет ненадежной характеристикой этой совокупности и ее практическое применение будет ограничено.

Для измерения вариации признака применяются различные абсолютные и относительные показатели. К абсолютным показателям вариации относятся размах колебаний, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.

Размах колебаний, или размах вариации, представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности:

R = x_max - x_min

Безусловным достоинством этого показателя является простота расчета, но значение этого показателя зависит только от значений крайних точек совокупности. На практике он находит применение в предупредительном контроле качества продукции.

Точнее характеризует вариацию признака показатель, учитывающий отклонения значений признака отдельных единиц совокупности от средней величины. К таким показателям относятся среднее линейное отклонение, дисперсия и среднее квадратическое отклонение.

Среднее линейное отклонение представляет собой среднюю величину из отклонений вариантов признаков от их средней.

Дисперсия это средний квадрат отклонений от индивидуальных значений признака от их средней величины.

Среднее квадратическое отклонение представляет собой корень квадратный из среднего квадрата отклонений отдельных значений признака от их средней.

Так как алгебраическая сумма отклонений индивидуальных значений признака от средней арифметической (согласно нулевому свойству) всегда равна нулю, то для расчета среднего линейного отклонения используется арифметическая сумма отклонений, т.е. суммируются абсолютные значения индивидуальных отклонений значений признака независимо от знака.

Формулы для расчета абсолютных показателей вариации приведены в табл.

Показатели	Формулы расчета
простая	взвешенная
1. Среднее линейное отклонение (d)	d=	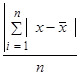d=
2. Дисперсия (σ 2)	σ 2=	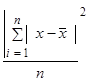σ 2=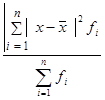
2а. Преобразованная формула для расчета дисперсии	σ 2=	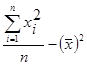σ 2=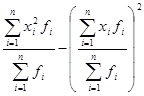
3. Среднее квадратическое отклонение (σ)	σ =	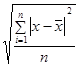σ =