
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Относительные показатели вариации
|
|
При сравнении колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической пользуются относительными показателями вариации. Эти показатели вычисляются как отношение абсолютных показателей вариации к соответствующей характеристике центра распределения — средней арифметической или медиане. Используя в качестве абсолютного показателя вариации размах вариации, среднее линейное отклонение, среднее квадратическое отклонение и квартильное отклонение, получим относительные показатели колеблемости (чаще всего они выражаются в процентах):
Коэффициент осцилляции: 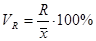
Относительное линейное отклонение: 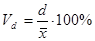
Коэффициент вариации: 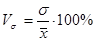
Относительный показатель квартальной вариации: 
Наиболее часто применяемый показатель относительной колеблемости — коэффициент вариации. Его используют не только для сравнительной оценки вариации разных признаков или в различных совокупностях, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких нормальному).
Расчет дисперсии в ряде случаев является затруднительным, поэтому логично, используя свойства дисперсии, упростить ее расчеты. Применяют два способа для упрощенного расчета дисперсии: способ отсчета от условного нуля и способ моментов.
По первому способу: 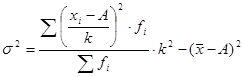 ,
,
где к-интервал,
А-условный нуль, в качестве которого удобно использовать середину интервала с наибольшей частотой.
По второму способу:
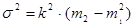 ,
,
где к-интервал,
m1= 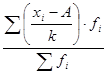 ; m2=
; m2= 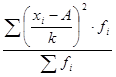
Покажем расчет дисперсии разными способами на примере распределения пользователей услуг связи по уровню среднемесячных расходов на услуги связи х (табл.5)
| x | f | x· f | 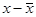
| (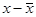 )2 )2
| (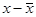 )2f )2f
| x2 | x2f | 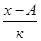
| 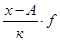
| 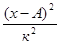
| 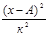 f f
|
| -22 | -2 | -80 | |||||||||
| -12 | -1 | -100 | |||||||||
| -2 | |||||||||||
| Итого | – | – | – | - | – |
Средние расходы пользователей на оплату услуг в месяц составляют:
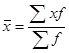 =81000/500=162 руб.
=81000/500=162 руб.
обычный способ расчета дисперсии 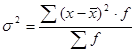 =68000/500=136;
=68000/500=136;
отсчет от условного нуля 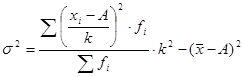
В качестве условной величины принят серединный вариант А=160, к=10
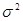 =(700· 100/500)-(162-160)2=140-4=136
=(700· 100/500)-(162-160)2=140-4=136
способ моментов
m1= 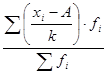 =100/500=0, 2; m2=
=100/500=0, 2; m2= 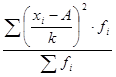 =700/500=1, 4
=700/500=1, 4
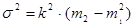 =100(1, 4-0, 04)=136
=100(1, 4-0, 04)=136
Среднее квадратическое отклонение равно 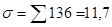 руб. коэффициент вариации 11, 7· 100/162=7, 2%, что свидетельствует об однородности совокупности пользователей услуг связи по уровню среднемесячных расходов на их оплату.
руб. коэффициент вариации 11, 7· 100/162=7, 2%, что свидетельствует об однородности совокупности пользователей услуг связи по уровню среднемесячных расходов на их оплату.
Расчеты дисперсии разными способами дают одинаковые результаты, что позволяют исследователю выбрать наиболее эффективный способ.