Проверка гипотезы о соответствии эмпирического распределения теоретическому

Расхождения между частотами эмпирического и теоретического распределений могут быть несущественными и объяснены случайностями выборки, а могут быть существенными при несоответствии законам распределения. Чтобы дать обоснованное объяснение причин расхождения между эмпирическими и теоретическими частотами, обращаются к критериям соответствия или согласия. К ним относятся критерии Пирсона, Романовского, Колмогорова, Ястремского и др.

Одним из наиболее часто употребляемых критериев согласия является критерии 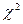(«хи-квадрат»), предложенный К. Пирсоном:

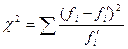
где 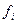и 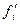–частоты эмпирического и теоретического распределения в определенном интервале.

Чем больше разность между наблюдаемыми и теоретическими частотами, тем больше критерий 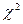. Чтобы отличить существенность различий частот эмпирического и теоретического распределений, рассчитанное значение критерия 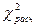сравнивают с табличным 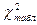при соответствующем числе степеней свободы и заданной вероятности (уровне значимости).

Число степеней свободы равно a= h - l, где h. — число групп; l — число условий, которые должны выполняться при вычислении теоретических частот. Для расчета теоретических частот кривой нормального распределения по формуле

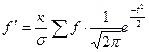
необходимо знать три параметра , , , поэтому число степеней свободы равно a= h -3

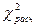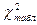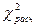
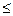
Если > , то расхождение между эмпирическими и теоретическими частотами существенно и его нельзя объяснить случайными колебаниями выборочных данных. В этом случае гипотеза о соответствии эмпирического и теоретического распределения отвергается. Если 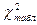, то возможное расхождение частот объясняется случайностями выборочного наблюдения и гипотеза о соответствии распределений принимается.

Критерии Пирсона эффективен при значительном числе наблюдений (п 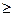50), причем частоты всех интервалов должны насчитывать не менее пяти единиц (при меньшем количестве интервалы объединяют), а число интервалов (групп) должно быть большим (h > 5), поскольку оценка 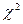зависит от числа степеней свободы.

Пример. Проверить нулевую гипотезу о соответствии распределения специалистов связи по уровню заработной платы нормальному закону. Расчетные величины для определения критерия Пирсона приведены в табл. 3.

Расчетное значение критерия Пирсона 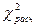⁼= 7, 12. При числе степеней свободы h-3 = 9-3 = 6 и уровне значимости 0, 05 = 12, 59. (см. приложение 5)

Так как 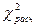‹ 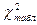гипотезу осоответствии эмпирического распределения нормальному не следует отвергать, т.е. данное распределение соответствует закону нормального распределения.