В.И. Романовский предложил близость эмпирического распределения к кривой нормального распределения оценивать по отношению

,

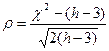где h – число групп

Если отношение больше 3, то расхождение частот эмпирического и нормального распределений нельзя признать случайным и гипотезу о нормальном законе распределения следует отвергнуть. Если отношение меньше или равно 3, то можно принять гипотезу о нормальном характере распределения данных.

Для рассматриваемого примера отношение Романовского 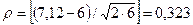, что существенно меньше 3 и дает право не отвергать гипотезу о нормальном законе распределения специалистов связи по уровню заработной платы.

А.Н. Колмогоров предложил для определения соответствия между эмпирическим и теоретическим нормальным распределениями использовать максимальную разность накопленных частот этих рядов. Для проверки гипотезы о соответствии эмпирического распределения закону нормального распределения рассчитывают критерии согласия 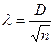, где D — максимальная разность между кумулятивными (накопленными) эмпирическими и теоретическими частотами n— численность единиц совокупности.

Таблица 3

Расчет величин для определения критериев согласия

Середина интервалов заработной платы х, руб.	fi		fi - fi	(fi - fi)2		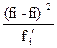Накопленная частота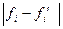
Фактическая	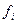Теоретическая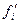
		1, 2	0, 8	0, 64	0, 53		1, 2	0, 8
		4, 5	2, 5	6, 25	1, 39		5, 7	1, 3
		10, 2	2, 8	7, 84	0, 77		15, 9	4, 1
		19, 8	-2, 8	7, 84	0, 40		35, 7	2, 7
		26, 0	-8, 0	64, 0	2, 46		61, 7	6, 7
		26, 0	5, 0	25, 0	0, 96		87, 7	1, 7
		19, 8	2, 2	4, 84	0, 24		107, 5	0, 5
		10, 2	1, 8	3, 24	0, 32		117, 7	2, 3
		4, 5	0, 5	0, 25	0, 05		122, 2	2, 8
Итого		–	–	–	7, 12	–	–	–

По специальной таблице определяют Р(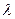) – вероятность достижения критерия согласия .

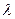Значения вероятностей для критерия согласия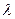

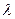
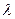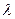
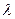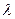
	Р()		Р()		Р()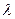
0, 3	1, 000	0, 8	0, 544	1, 5	0, 022
0, 4	0, 997	0, 9	0, 399	1, 8	0, 013
0, 5	0, 964	1, 0	0, 27	2, 0	0, 006
0, 6	0, 864	1, 1	0, 18	2, 1	0, 003
0, 7	0, 711	1, 2	0, 11	2, 3	0, 000

На основании значения Р(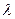) делают определенные выводы: если вероятность Р(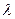) достаточно велика, то гипотеза о соответствии фактического распределения нормальному закону верная.

Максимальное расхождение накопленных эмпирических и теоретических частот равно 6, 7. Следовательно, 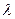=6, 7/ 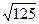=0, 6. Вероятность Р(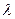) =0, 864. Т.е. вероятность достаточно велика, что позволяет утверждать, что фактическое распределение соответствует нормальному закону распределения.

Критерий Ястремского (L) может быть найден на основе следующего соотношения:

;
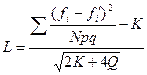