Розтягнутий стержень деформується , як це зображено на рисунку 2.1, і змінює свої подовжні та поперечні розміри на відповідні величини та (при стиску було б та ).

Міцність деталей машин. Оцінка міцності при простих деформаціях. Напруження і деформації при розтягу, згині, крученні. Діаграма розтягу. Допустимі напруження. Визначення реакцій в опорах. Побудова епюр.

Необхідним етапом оцінки міцності та жорсткості деталі є аналіз внутрішніх сил. Для визначення внутрішніх сил використовується метод перерізів. Суть цього методу визначається послідовністю таких операцій (рисунок 1.1):

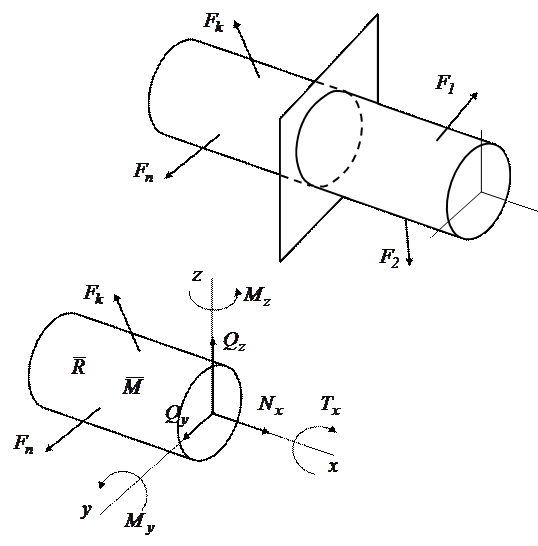Рисунок 1.1 – Метод перерізів. Внутрішні силові фактори.

1) умовно робимо переріз у місці визначення внутрішніх сил;

2) відкидаємо одну з двох частин перерізаної деталі;

3) дію відкинутої частини на залишену замінюємо внутрішніми силами. Ці сили зрівноважуються зовнішніми силами, що прикладені до залишеної частини;

4) визначаємо невідомі внутрішні сили з рівнянь рівноваги.

У загальному випадку просторової задачі система внутрішніх сил (рисунок 1.1 б) зводиться до головного вектора сил 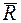, прикладеного у центрі ваги перерізу, та головного моменту 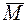, які розкладаємо по осях координат

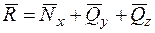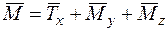; . (1.1)

Шість внутрішніх силових факторів, що виникають у перерізі деталі в загальному випадку, мають такі назви:

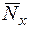– подовжня сила (або нормальна);

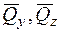- поперечні сили;

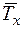– крутний момент;

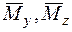– згинальні моменти.

Розглянемо далі питання про основні деформації. Із практики відомо, що під час експлуатації елементи конструкцій зазнають таких основних деформацій.

1. Розтяг – цієї деформації зазнають, наприклад, канати, троси, ланцюги, стержень тоді, коли вздовж його осі прикладені протилежно напрямлені сили. Ці деталі при навантаженні подовжуються.

2. Стиск – на стиск працюють, наприклад, колони, цегляна кладка, пуансони штампів, стержні ферм, які при стисканні вкорочуються.

Осьовим (центральним) розтягом або стиском брусу – називається такий простий вид навантаження, при якому єдиним внутрішнім силовим фактором у поперечному перерізі цього стержня є внутрішня подовжня сила .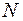

Простіше за все цей вид навантаження можна реалізувати, якщо прикласти до стержня зовнішні сили , лінія дії котрих збігається з його віссю

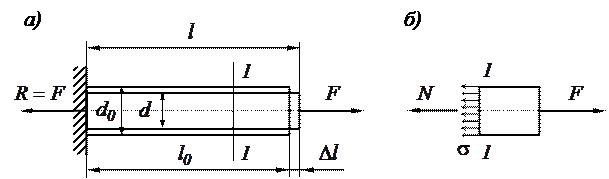Рисунок 2.1 – Модель розтягу брусу

Для визначення внутрішньої подовжньої сили 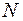застосуємо метод перерізів (рисунок 2.1 б).

З умов рівноваги уявно відрізаної частини стержня отримаємо: .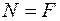

У загальному випадку, коли зовнішніх сил декілька, маємо правило:

Подовжня сила 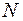у поперечному перерізі стержня чисельно дорівнює алгебраїчній сумі проекцій на вісь стержня зовнішніх сил, розташованих
з однієї сторони перерізу.

Правило знаків: 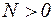, якщо вона розтягує (направлена від перерізу);

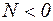, якщо вона стискає (направлена до перерізу).

У поперечних перерізах діють тільки рівномірно розподілені (гіпотеза Бернуллі) нормальні напруження σ, що можуть визначатися за формулою

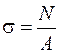, (2.1)

де 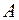– площа перерізу.

Розтягнутий стержень деформується, як це зображено на рисунку 2.1, і змінює свої подовжні та поперечні розміри на відповідні величини та (при стиску було б та).

Відносні деформації:

подовжня 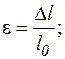(2.2)

поперечна 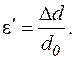(2.3)

Експерименти свідчать, що при навантаженні у відповідних межах для більшості матеріалів можна прийняти:

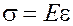. (2.5)

Ця залежність має назву закон Гука і формулюється таким чином:

Нормальні напруження прямо пропорційні лінійним деформаціям.

Сучасні машини, зазвичай, автоматично вимірюють навантаження і абсолютне подовження 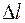і записують діаграму розтягу .

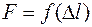Для прикладу розглянемо детально діаграму розтягу маловуглецевої сталі.

Ділянка 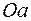– зона пропорційності, де виконуються пропорційні співвідношення між 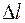та 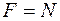або між 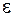та 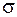.