
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построим одноиндексную математическую модель задачи линейного программирования.
|
|
Задание № 1
Оптимизация методом линейного программирования
Необходимо выполнить следующие задачи:
1. Построить одноиндексную математическую модель задачи линейного программирования. В модели необходимо указать единицы измерения всех переменных, целевой функции и каждого ограничения. Решить задачу с использованием Microsoft Excel 2003, 2007 или 2010.
2. Провести анализ на чувствительность.
3. Построить и решить двойственную задачу линейного программирования.
Торговая фирма для продажи товаров трех видов использует ресурсы: время и площадь торговых залов. Затраты ресурсов на продажу одной партии товаров каждого вида даны в таблице.
| Ресурсы | Вид товара | Объем ресурсов | ||
| Время, чел.-ч | 0, 5 | 0, 7 | 0, 6 | |
| Площадь, кв.м | 0, 1 | 0, 3 | 0, 2 |
Прибыль, получаемая от реализации одной партии товаров 1-го вида – 5 усл.ед., 2-го вида – 8 усл.ед., 3-го вида – 6 усл.ед.
Определить оптимальную структуру товарооборота, обеспечивающую фирме максимальную прибыль.
Решение
Построим одноиндексную математическую модель задачи линейного программирования.
Объектом моделирования является процесс получения максимальной прибыли, а целью – оптимизация структуры товарооборота.
Задача относится к классу оптимизационных задач. Математическая модель для задач такого класса состоит в построении целевой функции, для которой надо найти экстремум, при ограничениях.
Для данной задачи цель построения модели – максимизация прибыли от реализации партий товаров при соблюдении требований к общим нормам затрат ресурсов. Неизвестной является оптимальная структура товарооборота, обеспечивающая фирме максимальную прибыль.
Для решения поставленной задачи следует обозначить через х1, х2, х3 -количество партий товара 1-го, 2-го и 3-го вида соответственно (шт.). Общую прибыль от реализации товаров можно определить по формуле:
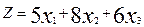 (усл.ед.).
(усл.ед.).
Функция Z называется целевой, ее следует максимизировать. На целевую функцию накладываются следующие ограничения:
- Количество реализованной продукции не может быть отрицательным.
- Количество используемых ресурсов не может превышать количество имеющихся ресурсов.
- На продажу 1-го вида товара затрачивается времени 0, 5 чел.-ч; для продажи товара 2-го вида – 0, 7 чел.-ч; для 3-го вида товара – 0, 6 чел.-ч. Время на реализацию всех 3-х видов товара не должно превышать 370 чел.-ч.
- Для продажи 1-го вида товара необходимо 0, 1 кв.м площади торговых залов; для продажи товара 2-го вида – 0, 3 кв.м; для 3-го вида товара – 0, 2 кв.м. Общая площадь торговых залов для реализацию всех 3-х видов товара не должно превышать 90 кв.м.
Таким образом, накладываются следующие ограничения:
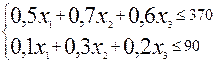
Математическая модель задачи: найти структуру товарооборота (X1, Х2, Х3), обеспечивающую максимальную прибыль фирме:

при ограничениях:
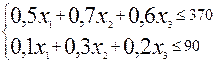
где по смыслу задачи:
x1 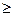 0, x2
0, x2 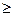 0, x3
0, x3 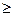 0.
0.