
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Итак, в этой модели четыре значения спроса соответствуют четырем состояниям природы, а количество закупаемых рождественских елок является решением
|
|
Итак, в этой модели четыре значения спроса соответствуют четырем состояниям природы, а количество закупаемых рождественских елок является решением. В таблице 1 представлена матрица доходов для данной модели.
Таблица 1
| Решение | Состояние природы | |||
| -2200 | -6200 | |||
| -400 | -4400 | |||
| -3000 | -1000 | |||
| -8000 | -6000 |
Доходы вычисляются по следующей формуле:
Доход = 20*Количество проданных елок - 10*Количество закупленных елок -8*Неудовлетворенный спрос
Используем данную формулу для вычисления ожидаемого результата (дохода) для каждого решения и выберем то решение, для которого ожидаемый доход будет наибольшим (рис.1).
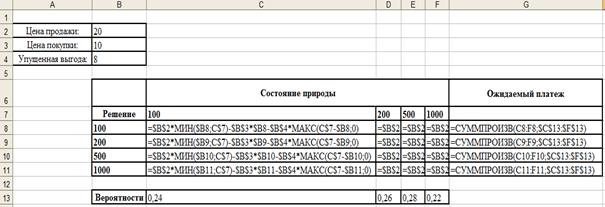
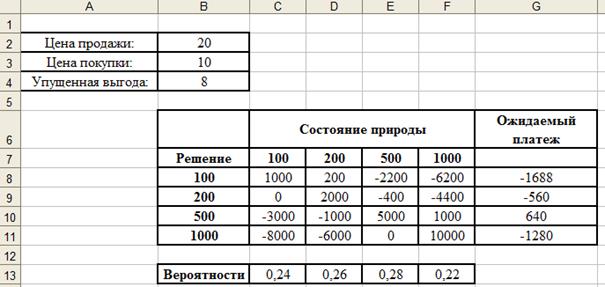
Рис. 1. Базовый лист
Так как максимальное значение имеет ЕК3, оптимальным решением будет закупить 500 елок.
Проведем анализ на чувствительность к изменению значений цены на непроданные на Рождество елки.
Один из способов анализа чувствительности заключается в задании разных значений упущенной выгоды (изменяя цены на непроданные на Рождество елки), перерасчете матрицы доходов, повторном вычислении ожидаемых доходов и выборе на их основе нового оптимального решения.
Значения упущенной выгоды будем изменять от 0 до 20 долларов с шагом в 1 доллар. Для создания таблицы подстановки выполним следующие действия.
1. Скопируем данные с рабочего листа Задача_3 на лист Анализ чувствительности.
2. Вводим, например, в столбец В, начиная с ячейки В7, значения от 0 (начальное значение упущенной выгоды) до 20 с шагом 1.
3. В ячейку С6 введите формулу =G8, которая даст значение ожидаемого платежа для решения 100. В ячейки D6: F6 вводим формулы =G9, =G10, =G11, которые дадут значения ожидаемых платежей для решения 200, 500 и 1000 соответственно.
4. Выделяем диапазон В6: F37 и выполняем команду МS Ехсе1 2007 Данные/ Анализ «что - если»/ Таблица данных... В диалоговом окне Таблица данных в поле Подставлять значения по строкам в вводим $В$4. Результат представлен на рисунке 2.
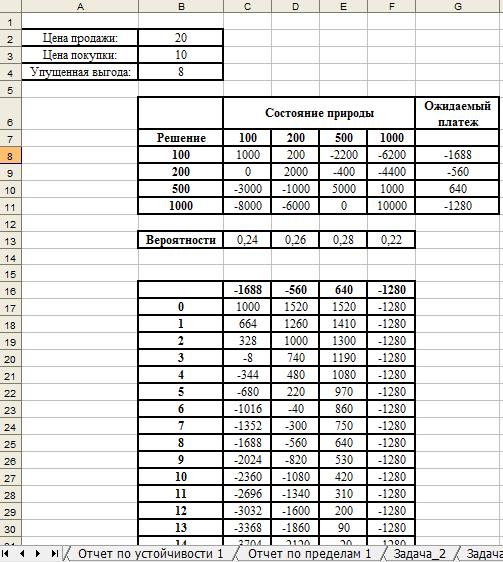
Рис. 2. Таблица подстановки
5. Результаты, представленные в таблице подстановки, представим в графическом виде (рис. 3).
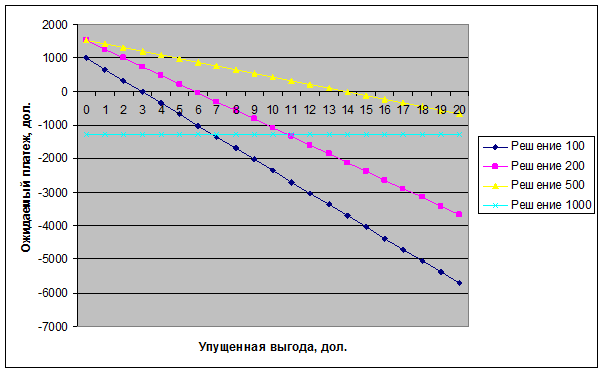
Рис. 3. График для анализа чувствительности
На построенном графике видно, что при возрастании значения упущенной выгоды, ожидаемые платежи убывают (для решения 100, 200 и 500) или остаются постоянными (для решения 1000).
Если значение упущенной выгоды меньше 14 долларов, то оптимальным будет решение 500.
Таким образом, нет необходимости знать точное значение упущенной выгоды, чтобы определить оптимальное решение достаточно знать, будет ли оно больше или меньше 14 долларов.
2. Принятие решений в условиях неопределенности
В условиях неопределенности лицо, принимающее решение, не знает вероятностей наступления того или иного состояния природы. Рассмотрим следующие критерии:
1) критерий Лапласа;
2) критерий Сэвиджа;
3) критерий Гурвица;
4) минимаксный критерий.
2.1. Критерий Лапласа.
В модели торговой сети компании «Елочка» из предположения о равной вероятности всех состояний природы следует, что вероятности всех четырех событий (соответствующих разным величинам спроса) будут одинаковыми и равными 0, 25. Далее можно пересчитать модель принятия решения в условиях риска с этими вероятностями и получить ожидаемые значения доходов. После такого перерасчета оптимальным будет решение 3, в соответствии с которым следует закупить 500 рождественских елок (рис. 4).
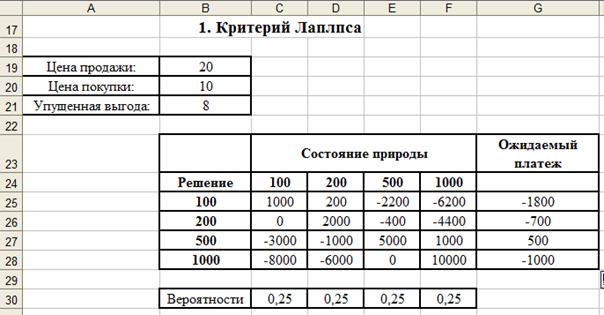
Рис. 4. Решение с помощью критерия Лапласа
2.2. Минимаксный (максиминный) критерий.
Этот критерий является наиболее осторожным (критерий осторожного наблюдателя (критерий Вальда)), так как основывается на выборе наилучшей из наихудших возможностей.
В модели торговой сети компании «Елочка» каждому решению ставится в соответствие минимальное значение в его строке в матрице доходов. В качестве искомого решения выбираем то решение, которому будет соответствовать максимум минимального значения дохода. В нашем следует закупить 500 рождественских елок (рис. 5).
Максиминный критерий часто используется в ситуациях, когда принимающий решение менеджер не может допустить самого худшего исхода.
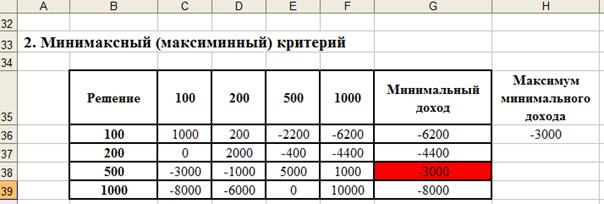
Рис. 5. Решение с помощью максиминного критерия
2.3. Критерий Сэвиджа.
Критерий минимакса настолько «пессимистичен», что иногда может приводить к нелогичным выводам.
Для модели торговой сети компании «Елочка» на основе матрицы сожаления построим таблицу максимальных потерь, выбрав для каждого решения максимальное значение в его строке в матрице сожаления (рис. 6).
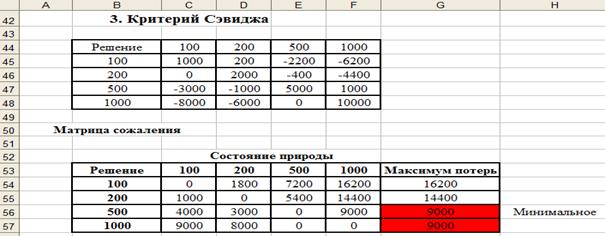
Рис. 6. Решение с помощью критерия Сэвиджа
Теперь выбираем решение, которое минимизирует максимум потерь. В данном случае критерий минимаксных потерь укажет на решение 500 или 1000.
2.4. Критерий Гурвица.
Этот критерий охватывает ряд различных подходов к принятию решений: от наиболее оптимистичного до наиболее пессимистичного.
Критерий Гурвица основан на следующих двух предположениях:
- среда может находиться в самом невыгодном состоянии с вероятностью 1-а;
- в самом выгодном - с вероятностью а, где а - коэффициент доверия (или показатель оптимизма).
При а=1 критерий слишком оптимистичный, при а = 0 он слишком пессимистичный. Значение а между 0 и 1 может определяться в зависимости от склонности ЛПР к пессимизму или оптимизму. При отсутствии ярко выраженной склонности а=1/2 представляется наиболее разумным.
Для модели торговой сети компании «Елочка» примем а=1/2 (рис. 7).
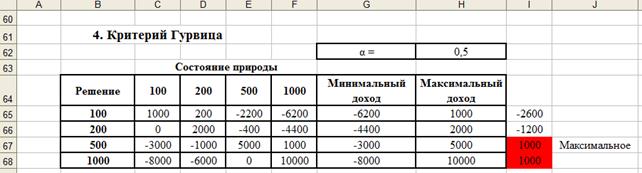
Рис. 7. Решение с помощью критерия Гурвица
Таким образом, на основании всех рассмотренных критериев, можем сделать вывод, что оптимальное решение заключается в закупке 500 елок.
Список использованной литературы
1. Алесинская, Т.В. Учебное пособие по решению задач по курсу «Экономико-математические методы и модели» / Т.В. Алесинская. – Таганрог: Изд-во ТРТУ, 2002 - 153с.
2. Вентцелъ Е.С. Исследование операций: задачи, принципы, методология / Е.С. Вентцель. М., 1980.
3. Замков О.О. Математические методы в экономике: учебн. / О.О. Замков, А.В. Толстопятенко, Ю.Н. Черемных. М., 1998.
4. Косоруков, О.А. Исследование операций: учебник / О.А. Косоруков, А.В. Мищенко. – М.: Издательство «Экзамен», 2003.– 448 с.
5. Кремер, Н.Ш. Исследование операций в экономике / Н.Ш. Кремер. – М.: ЮНИТИ, 2000.
6. Кундышева Е. С. Математическое моделирование в экономике. Учебное пособие/ Под науч. Ред. Проф. Суслакова Б. А. - М.: Издательско – торговая корпорация “Дашков и К”, 2004. - 352с.
7. Минюк Е. А., Ровба Е. А., Кузьмич К. К. Математические методы и модели в экономике. Учебное пособие - Минск: ТетраСистемс, 2002. - 432с.
8. Мур, Дж. Экономическое моделирование в Microsoft Excel / Дж. Мур, Л. Уэндерфорд. – 6-е изд., испр. и доп. / пер. с англ. – М.: Издательский дом «Вильямс», 2004. – 1024с.
9. Таха, Х.А. Введение в исследование операций / пер. с англ. Х.А. Таха. –7-е изд., испр. и доп. – М.: Издательский дом «Вильямс», 2005. – 912 с.
10. Цаплина, С.А. Методы математического моделирования [Текст]: учеб. пособие / С.А. Цаплина. - Архангельск: Изд-во АГТУ, 2007.-88 с.
11. Эдоус, М. Методы принятия решений / М. Эдоус, Р. Стэнсфилд. – М.: Аудит, 1997.