Матриця-стовпець та матриця-рядок

Типи матриць

Матриця яка складається з одного стовпця чи одного рядка, називається відповідно матриця-стовпець чи матриця-рядок. Матрицю-стовпець і матрицю-рядок називають також векторами.

Будемо записувати вектори в такій формі:

Х = 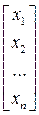- матриця-стовпець (вектор) (1.18)

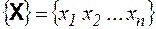- матриця-рядок (також вектор) (1.19)

Квадратна матриця.

Матриця, кількість рядків і стовпців якої є n, називається квадратною матрицею порядку n. Сукупність елементів з індексами ii (i = 1, 2, 3..., n) утворює головну діагональ квадратної матриці.

Діагональна матриця. Квадратна матриця, всі елементи якої поза головною діагоналлю дорівнюють нулю, тобто

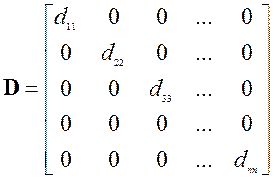: (1.20)

Якщо в матриці D всі елементи рівні між собою 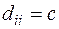, то діагональна матриця називається скалярною.

Одинична матриця.

Якщо в діагональній матриці 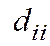= 1, i = 1, 2, …, n, а всі інші елементи дорівнюють нулеві, то така матриця називається одиничною порядку n. Позначається одинична матриця символом Е. Наприклад:

Е = є одиничною матрицею порядку 4 (1.21)

Одинична матриця в матричному численні відіграє роль, у деякій мері, аналогічну одиниці в скалярних арифметичних операціях.

Нульова матриця.

Матриця, всі елементи якої дорівнюють нулю, називаються нульовою. Позначається нульова матриця цифрою нуль: 0. Зауважимо, що нульова матриця може мати будь-який розмір m × n на відміну від одиничної, яка завжди квадратна.

Стрічкова матриця.

Якщо в квадратній матриці порядку m відмінними від нуля є лише елементи, розміщені на головній діагоналі, і на прилягаючій до неї з кожної сторони (зверху і знизу) k рівнобіжних лініях, то така матриця називається стрічковою, із шириною стрічки k:

(1.22)

Верхня і нижня трикутні матриці.

Квадратна матриця називається верхньою (нижньою) трикутною, якщо всі елементи, розташовані під (над) головною діагоналлю дорівнюють нулю:

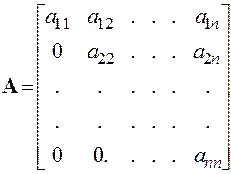верхня трикутна матриця (1.23)

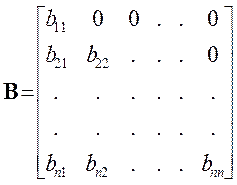(1.24)

Матриця В (1.24) є нижньою трикутною матрицею

Симетрична матриця.

Квадратна матриця називається симетричною, якщо її елементи, розташовані симетрично щодо головної діагоналі, дорівнюють один одному, тобто, якщо має місце рівність:

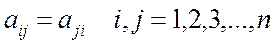(1.25)

1.5.3. Операції над матрицями.

Рівність матриць.

Дві матриці рівні, якщо вони, мають однакові розміри і характеризуються рівністю, по парам, усіх однаково розташованих елементів, тобто:

A = B, якщо 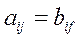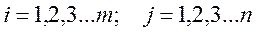(1.26)