
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Приклад множення двох матриць.
|
|
Задано дві матриці: А розміром 3х3 та В розміром 3х2
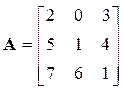
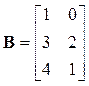
Знайти добуток А·В
Позначимо результуючу матрицю C. Обчислимо послідовно її елементи:
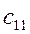 = 2 3 1+0 3 3+3 3 4 = 14 = 2 3 1+0 3 3+3 3 4 = 14
| 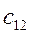 = 2 3 0+0 3 2+3 3 1 = 3 = 2 3 0+0 3 2+3 3 1 = 3
|
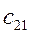 = 5 3 1+1 3 3+4 3 4 = 24 = 5 3 1+1 3 3+4 3 4 = 24
| 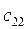 = 5 3 0+1 3 2+4 3 1 = 6 = 5 3 0+1 3 2+4 3 1 = 6
|
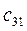 = 7 3 1+6 3 3+1 3 4 = 29 = 7 3 1+6 3 3+1 3 4 = 29
| 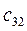 = 7 3 0+6 3 2+1 3 1 = 13 = 7 3 0+6 3 2+1 3 1 = 13
|
У результаті одержимо:
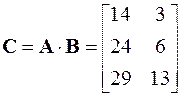
Операції множення матриць не піддаються комутативному закону. У загальному випадку A·B 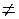 B·A. Якщо виконується співвідношення A·B = B·A, то матриці A і B мають спеціальну назву: комутуючи переставні.
B·A. Якщо виконується співвідношення A·B = B·A, то матриці A і B мають спеціальну назву: комутуючи переставні.
Характерні випадки множення двох матриць
Множення матриці на матрицю-стовпець дає матрицю-стовпець (вектор):
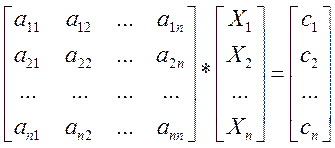 (1.32)
(1.32)
Множення матриці-рядка на матрицю-стовпець дає скаляр:
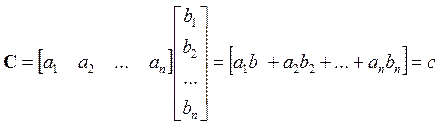 (1.33)
(1.33)
Матриця С має тільки один елемент, тобто є скаляром.
Множення матриці-стовпця на матрицю-рядок дає матрицю розміром m 3 n, де m – розмір матриці-стовпця, n - розмір матриці-рядка:
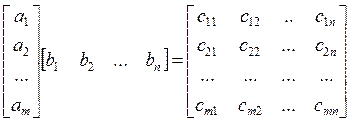 (1.34)
(1.34)
На закінчення, відзначимо одну цікаву особливість множення матриць. Виявляється, що добуток двох ненульових матриць може дати нульову матрицю. З факту, що A·B=0 ще зовсім не впливає, що A чи B=0.
Наприклад:
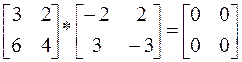
Транспонування матриць. Перетворення матриці A, що складає в заміні рядків стовпцями (чи стовпців рядками) називається транспонуванням. Отримана внаслідок такого перетворення матриця називається транспонованою до матриці A і позначається звичайно тим же символом, з додаванням верхнього індексу «Т»: A Т.
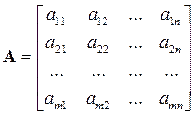
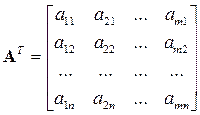 (1.35)
(1.35)
Таким чином, матриця розміром 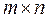 після транспонування буде мати розмір
після транспонування буде мати розмір 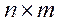 .
.