
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Параметри періодично змінних сигналів
|
|
Кожний періодичний сигнал, наприклад, напруга u (t), незалежно від форми характеризується такими параметрами:
• амплітудним (максимальним, піковим) значенням Um за період;
• середнім значенням за період Uср або сталою складовою U0:
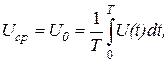 (2.1)
(2.1)
де Т – період;
• середнім випрямленим значенням (СВЗ) Uсв:
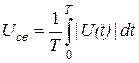 ; (2.2)
; (2.2)
• середнім квадратичним (діючим, ефективним) значенням (СКЗ) U:
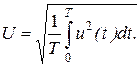 (2.3)
(2.3)
Середнє Uср=U0, середнє випрямлене Uсв і середнє квадратичне U значення називають інтегральними значеннями змінних сигналів.
Крім цих величин, періодичні сигнали характеризуються ще коефіцієнтом амплітуди kа та коефіцієнтом форми кривої kф, які пов’язують між собою амплітудне Um, середнє квадратичне U і середнє випрямлене Uсв значення змінних сигналів:
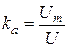 , (2.4)
, (2.4)
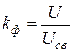 , (2.5)
, (2.5)
а також коефіцієнтом усереднення kу, який дорівнює добутку коефіцієнтів форми та амплітуди – kу = kа× kф і є залежним від них.
Вимірявши амплітудне Um, середнє квадратичне U і середнє випрямлене Uсв значення змінних сигналів можна визначити ці коефіцієнти, між якими справедливе наступне співвідношення kу ≥ kа ≥ kф ≥ 1.
На практиці користуються двома незалежними коефіцієнтами – коефіцієнтом амплітуди kа та коефіцієнтом форми кривої kф, значення яких для найпоширеніших у вимірювальній техніці сигналів різної форми наведені в табл. 2.1.
Отже, для відомої форми кривої сигналу при відомому значенні однієї із його характеристик (Um, U чи Uсв), можна вирахувати інші, використавши значеннякоефіцієнта амплітуди kа та коефіцієнта форми кривої kф.
Будь-який періодичний сигнал u (t), що задовольняє умови Дирихлє, тобто на кожному скінченому інтервалі він є обмежений, кусково-неперервний і має скінчене число екстремумів, може бути розкладений в тригонометричний ряд Фур¢ є:
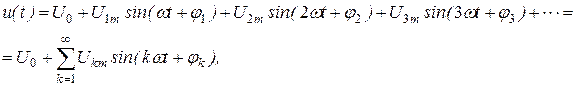 (2.6)
(2.6)
де U0 – стала складова сигналу або нульова гармоніка; U 1 m sin(wt+j 1 ) – основна синусоїда або перша гармоніка; 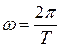 - основна частота, рад/с; Т – період сигналу, с; jk – початкова фаза k -тої гармоніки, рад; Ukm sin(kwt+jk) – k -та гармоніка (всі складові при k ³ 2 називаються вищими гармоніками).
- основна частота, рад/с; Т – період сигналу, с; jk – початкова фаза k -тої гармоніки, рад; Ukm sin(kwt+jk) – k -та гармоніка (всі складові при k ³ 2 називаються вищими гармоніками).
Середнє квадратичне значення періодичного складного сигналу, розкладеного у ряд Фур’є, тобто на n синусоїд (гармонік) визначається як
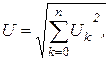 (2.7)
(2.7)
де Uk – середнє квадратичне значення k -тої гармоніки, включаючи сталу складову U0.
Таблиця 2.1
Значення коефіцієнтів амплітуди і форми для сигналів різної форми
| № з/п | Форма кривої сигналу | Коефіцієнт амплітуди kа | Коефіцієнт форми kф | ||||||||||||||
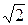
| 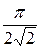 = 1, 11 = 1, 11
| ||||||||||||||||
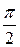
| |||||||||||||||||

  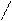 
      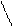 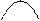 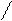 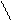   3 3
| 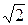
| 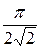
| |||||||||||||||
      4 4
| |||||||||||||||||

 
      
  5 5
| 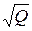
| 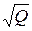
| |||||||||||||||
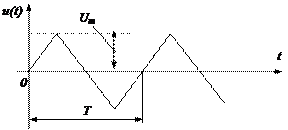 6 6
| 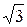
| 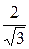
| |||||||||||||||
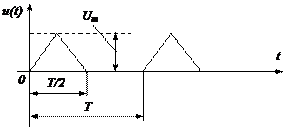 7 7
| 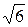
| 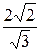
| |||||||||||||||
 8 8
| 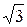
| 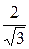
| |||||||||||||||
 9 9
| 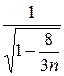
| 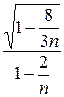
| |||||||||||||||

| 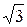
| 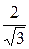
|

