
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Порядок выполнения работы. 2.1 Изучить содержание шестой и восьмой лекции курса.
|
|
Подготовка к работе
2.1 Изучить содержание шестой и восьмой лекции курса.
2.2 Изучить по литературе [1] содержание страниц 382-384, 354-357
Пояснения к работе
При решении самых разнообразных научно-технических задач возникает необходимость в определении зависимости функции от одного или нескольких аргументов. Например, необходимо рассчитать мощность радиосигнала в зависимости от расстояния или колебательный процесс в электрическом контуре.
При этом результаты расчета следует представить в виде массива чисел, заключив их в определенную таблицу. При подобных многократных расчетах по одной и той же формуле или алгоритму следует:
- во-первых, выбрать " шаг" или дискрет изменения аргумента:
- во-вторых, определить точность, с которой требуется рассчитывать значение того или иного параметра.
Иногда требуется рассчитать десятки, сотни и даже тысячи значений одной и той же функции в зависимости от значения аргумента.
В подобных случаях самый экономный путь решения задачи состоит в организации расчета в рамках определенного цикла. В таком цикле автоматическое обращение к функции производится согласно зашитому в программу алгоритму. При этом пользователь указывает только шаг. точность и количество вариантов расчета.
Порядок выполнения работы
4.1 Изучение способа орг анизации циклического расчета с использованием оператора цикла.
Самый простой способ организации циклического расчета состоит в использовании оператора цикла 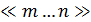 , пиктограмма которого расположена на математической панели инструментов " Матрица" После вызова щелчком этого оператора в него следует ввести значения нижнего и верхнего пределов
, пиктограмма которого расположена на математической панели инструментов " Матрица" После вызова щелчком этого оператора в него следует ввести значения нижнего и верхнего пределов
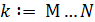
где 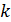 – дискретно на 1 изменяемый параметр, последовательно принимающий целые значения от целых
– дискретно на 1 изменяемый параметр, последовательно принимающий целые значения от целых 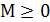 до
до 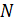 .
.
Причем при 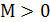 все значения функции при
все значения функции при 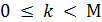 принимают значения, равные 0. Аргумент
принимают значения, равные 0. Аргумент 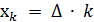 при циклическом расчете изменяется с " шагом" (дискретом)
при циклическом расчете изменяется с " шагом" (дискретом) 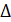 . значение которого может быть выбрано любым
. значение которого может быть выбрано любым
Задание 1.
Рассчитать с " шагом" 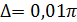 затухший колебательный процесс, описываемый функцией:
затухший колебательный процесс, описываемый функцией:
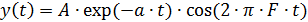
при 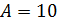 ,
, 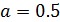 ,
, 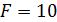 и
и  .
.
Сначала построим график непрерывной функции 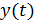 . Затем организуем цикл расчета с помощью записи
. Затем организуем цикл расчета с помощью записи 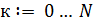 и выражений для аргумента
и выражений для аргумента 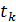 и дискретной функции
и дискретной функции 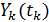 , полученной из непрерывной функции
, полученной из непрерывной функции 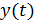 .
.
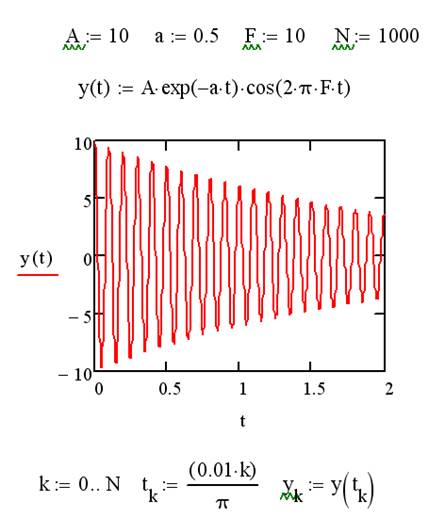
Строим график дискретной функции 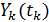 .
.
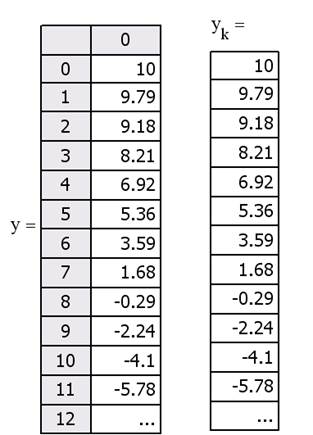
Вывод в виде таблицы дискретных значений 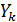 осуществляется путем записи
осуществляется путем записи 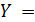 или
или 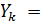 . По умолчанию на рабочий лист выводится 16 значений функции. Щелкнув по графику функции, обрамляют его рамкой и путем протаскивания вниз курсора расширяют таблицу до любого требуемого значения
. По умолчанию на рабочий лист выводится 16 значений функции. Щелкнув по графику функции, обрамляют его рамкой и путем протаскивания вниз курсора расширяют таблицу до любого требуемого значения 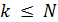 .
.
При протаскивании курсора вверх таблица наоборот сжимается. Таким же образом можно вывести и таблицу значений аргумента, сделав в рассматриваемом случае запись  .
.
4.2 Изучение способов определения корней алгебраических уравнений.
Возможны два способа нахождения корней алгебраического уравнения в среде " Mathcad". С помощью методов символьной математики и путем обращения к встроенной функции.
Задание 2.
Найти корни кубического уравнения
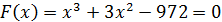 (1)
(1)
а) Пусть требуется найти решение с помощью методов символьной математики.
Открываем рабочий лист и записываем многочлен из уравнения (1)
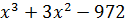
Выделяем в этом многочлене в любом члене один символ – переменную 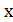 – путем перетаскивания курсора. Открываем меню " Символ", подменю " Переменные" (Variable), щелчок по опции " Вычислить".
– путем перетаскивания курсора. Открываем меню " Символ", подменю " Переменные" (Variable), щелчок по опции " Вычислить".
На рабочем листе появляется результат, записанный в форме вектора
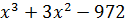
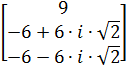
б) Решение путем обращения к встроенной функции.
Вновь записываем многочлен из уравнения (1):
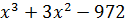
Выделяем в этом многочлене в любом члене один символ переменной 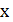 – путем протаскивания курсора, например, у
– путем протаскивания курсора, например, у 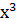 затемняем
затемняем 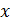 . Записываем вектор коэффициентов многочлена, для чего открываем меню " Символ", щелчок по опции " Коэффициенты" (Polynomial Coefficients).
. Записываем вектор коэффициентов многочлена, для чего открываем меню " Символ", щелчок по опции " Коэффициенты" (Polynomial Coefficients).
Перед вектором вставляем его имя  . Получаем результат:
. Получаем результат:
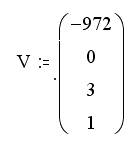
Следует отметить, что при отсутствии какого-либо члена, соответствующий ему коэффициент принимается равным 0.
Обращаемся к пиктограмме " Встроенная функция f(x)" на второй строке текстового окна – стандартной линейке. На появившемся после щелчка диалоговом окне в разделе " Категория функций" выбираем строку с надписью " Решение", а в разделе " Название функции" - polyroots (корни полинома).
После нажатия на кнопку " ОК" или " Вставить" на рабочем листе появляется название данной функции В скобки вписываем имя вектора коэффициентов V и вводим знак " =" После ввода знака равенства получаем результат в виде вектора:
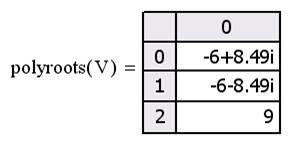
Точность полученного результата устанавливаем путем открытия меню " Формат", полменю " Результат" и выбора требуемого числа десятичных знаков в открывшемся окне.
Проводим проверку (check-up) полученных результатов. Для этого последовательно при каждом из полученных значений корня х, (переносим их методом копирования) вычисляем значение многочлена F(x). Близость к нулю действительной и мнимой частей Г(х) указывает на правильность полученных результатов
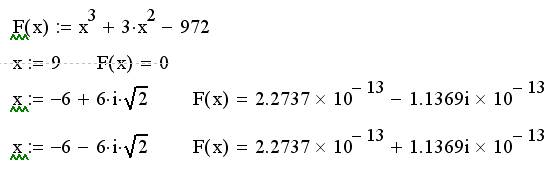
в) Записать произвольно любое алгебраическое уравнение третьей степени и найти его корни двумя методами.
4.3 Изучение способов определения корней трансцендентных уравнений.
В среде MathCAD возможны два способа нахождения корней трансцендентных уравнений:
· с помощью методов символьной математики согласно правилу 6;
· с помощью встроенной функции root в подменю f(x) меню «Вставка» согласно правилу 2.
Рассмотрим применение обоих методов на примере нахождения корней уравнения:
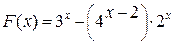
Общим для нахождения корней является только графический метод, состоящий в построении графика функции F(x).
Точки пересечения построенного графика с осью абсцисс и есть искомые действительные корни уравнения.
Поскольку неизвестно решение (значения х, при которых F(x) =0), то строим его график с целью приблизительного определения искомого действительного решения.
х: = -10 … +10
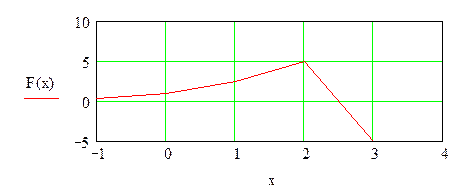
Рис. 4.3.1 Графическое решение
Из графика видно, что это решение, определяемое как точка пересечения графика с осью абсцисс, лежит в промежутке значений х = 2…3.
Решение по правилу 6
Записываем многочлен из уравнения (6.4):
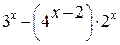
Выделяем (затемняем ■) в этом многочлене в любом месте символ переменной х – путем протаскивания курсора.
Открываем меню «Символ», подменю «Переменные» и делаем щелчок по опции «Вычислить».
На рабочем листе получается результат:
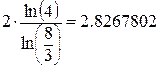
Решение по правилу 2:
Записываем уравнение:
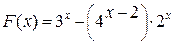
Вводим любое имя искомого решения и знак присвоения, например:
r: =,
после которого размещаем красный визир ±.
Обращаемся к пиктограмме «Встроенная функция f(x)» на 2-ой строке текстового окна – стандартной линейке.
На появившемся после щелчка диалоговом окне в разделе «Категория функций» выбираем строку с надписью «Решение», а в разделе «Название функций» - root (корни). После нажатия на кнопку «ок» или «Вставить» на рабочем листе появляется название данной функции с четырьмя черными прямоугольниками, которые следует заполнить:
r: = root (■, ■, ■, ■)
В первое окошко вписываем имя функций F(x), во второе – переменную х, в третье и четвертое – (а) нижний и (в) верхний пределы, внутри которых ищется решение. Запись приобретает вид:
r: = root (F(x), x, a, в),
(пределы согласно рисунку 6.1 установлены 0 и 3).
Вновь вводим искомое решение, но теперь со знаком равенства:
r =,
и сразу получаем результат.
r = 2, 8267802
Точность полученного результата устанавливаем путем открытия меню «Формат», подменю «Результат» и выбора требуемого числа десятичных знаков в открывшемся окне.
Проводим проверку полученного результата, для чего вычисляем значение функции F(x) при найденном значении корня.
x: = 2.8267802
F(x) = 2.287 · 10-7
Близость к нулю функции F(x) указывает на правильность полученного результата.
|