Лекция 4

Тема: МОМЕНТ ГИРОСКОПИЧЕСКОЙ РЕАКЦИЙ

При рассмотрении вопроса о прецессии гироскопа мы видели, что под действием приложенной внешней силы главная ось гироскопа движется не по направлению силы, а перпендикулярно ей и оказывает этой силе сопротивление.

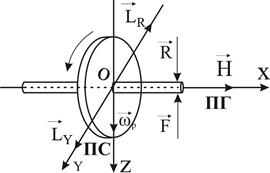Если, например, пальцем нажать на опоры главной оси гироскопа с некоторой силой F (рис.10), то со стороны опор этой оси к пальцу прикладывается противодействующая сила реакции R, уравновешивающая нажим, т.е. силу F Рис.10. Сила R реакции опор гироскопа называется гироскопической реакцией, а момент этой силы - моментом гироскопическое реакции, или гироскопическим моментом L_R. Силы F и R равны по величине, но противоположны по направлению. Поэтому момент гироскопической реакции равен по величине, но противоположен по направлению моменту L приложенной силы:

L_R= - L (27)

Рис.10

Угловая скорость прецессии определяется по формуле ω _Р =L/H отсюда:

L = ω _Р·H. (28)

Следовательно

L_R=- ω _Р H. (29)

Таким образом, момент гироскопической реакции равен произведению кинетического момента на угловую скорость прецессии и направлен в сторону, противоположную моменту внешней силы, вызвавшей прецессию гироскопа,

Для определения направления вектора гироскопического момента пользуются правилом, которое вытекает непосредственно из (рис. 10): направление вектора L_R таково, что он как бы стремится совместить по кратчайшему пути вектор кинетического момента Н гироскопа с вектором угловой скорости прецессии ω _Р.

Гироскопический момент препятствует главной оси гироскопа повороту в направлении действия силы.

Из формулы (29) следует, что появление гироскопического момента всегда обусловливается наличием двух вращений: прецессии гироскопа, которая, в свой очередь, возникает из действия на гироскоп момента внешней силы и вращения ротора.

Момент гироскопической реакции возникает при всяком вынужденном повороте гироскопа вокруг оси, не совпадающей с осью вращения. Чтобы убедиться в этом, достаточно попробовать повернуть руками главную ось гироскопа.

Тогда мы почувствуем, что эта ось сопротивляется повороту, стремятся вырваться из рук и оказывает на наши руки давление. По ощущению в руках мы убедимся, что при повороте в горизонтальной плоскости ось гироскопа давит на руки вертикальной парой сил, и наоборот.

Чтобы продемонстрировать появление гироскопического момента при вынужденном повороте, лишим гироскоп, показанный на рис.11, возможности поворачиваться вокруг оси У. Такой гироскоп будет иметь две степени свободы: вокруг оси X и вокруг оси Z. Возьмем прибор в руки и будем поворачивать его вместе с подставкой, вокруг оси У с некоторой угловой скоростью ω _ву. Такой поворот гироскопа называется вынужденным поворотом, или вынужденной прецессией.

Мы увидим, что гироскоп, совершая вынужденную прецессию вокруг оси У, начнет одновременно поворачиваться вокруг оси Z. так, чтобы вектор Н кратчайшим путем совместился с вектором ω _ву (сверху этот поворот будет виден против движения часовой стрелки).

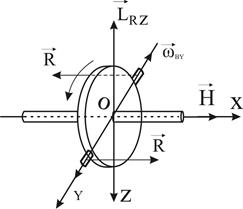Таким образом, на гироскоп передается пара сил R, устанавливающая его ось определенным образом. Момент этой пары является гироскопический моментом L_rz, возникающим вследствие вынужденной прецессии. В этом можно убедиться, определив направление вектора L_rz, в данном примере по правилу, которое приводилось выше.

Величина гироскопического момента при вынужденном повороте (вынужденной прецессии) гироскопа определится из формулы:

Рис.11 L_RZ = - ω _ву. (30)

Не вникая в физическую природу гироскопического момента, отметим, что он является следствием так называемых кориолисовых сил инерции, которые возникают при повороте вращающегося тела вокруг оси, не совпадающей с осью собственного вращения. В наших примерах гироскопический момент возникал при одновременных поворотах гироскопа: собственного вращения ротора вокруг оси X и прецессии (вынужденной прецессии) главной оси вокруг оси У или Z.

ЛЕКЦИЯ 5

Тема: УРАВНЕНИЯ ДВИЖЕНИЯ ГИРОСКОПА