Степенные средние

№ п/п	Вид степенной средней	Показатель степени (m)	Формула расчета
Простая (для несгруппированных данных)	Взвешенная (для сгруппированных данных)
	Арифметичекая
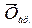
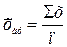
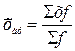
	Квадратическая
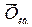
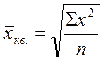
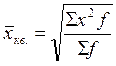
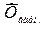
	Гармоническая	-1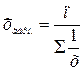
	Геометрическая

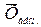
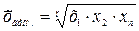
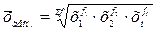
Средняя арифметическая простая применяется в тех случаях,
когда веса отсутствует или они равны между собой.

Средняя арифметическая взвешенная применяется, когда
значения осредняемого признака встречаются несколько раз.

Средняя квадратическая широко используется при оценке
вариации признака, при изучении взаимосвязи явлений.

Средняя гармоническая величина (обратная средней арифметической) применяется в тех случаях, когда неизвестны значения частот
у вариант ряда, зато имеются произведения этих вариант на соответствующие им частоты (w = xf).

Средняя геометрическая применяется для расчета среднего
коэффициента или темпа роста.

К структурным средним относятся мода, медиана, квартили, децили.

Мода (Мо) – это наиболее часто встречающееся значение признака
в данной совокупности (значение варианты с наибольшей частотой).

В дискретном ряду мода равна значению признака, которому
соответствует наибольшая частота.

В интервальном ряду мода определяется по формуле:

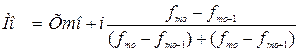
где:

Xmo – нижняя граница модального интервала

i – величина модального интервала

fmo – частота модального интервала

fmo- 1 – частота интервала, предшествующего модальному

fmo+ 1 – частота интервала, следующего за модальным

Модальным считается тот интервал, которому соответствует
наибольшая частота.

Медиана (Ме) – значение признака, которое находится в середине ранжированного (упорядоченного) ряда. Медиана делит статистическую совокупность на две равные части.

В интервальном вариационном ряду медиана определяется по
формуле

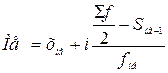
где:

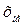- нижняя граница медианного интервала;

i - величина медианного интервала;

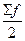- полусумма частот;

S 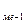- сумма накопленных частот до медианной частоты;

f 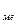- частота медианного интервала.

Медианным считается тот интервал, накопленная частота которого равна или превышает половину всех частот.

Квартили (Q)делят ранжированный ряд на четыре равные части.

Децили (D) делят ранжированный ряд на десять равных частей.

Показатели вариации характеризуют отклонения от средней
величины.

Для изменения величины вариации используются абсолютные и
относительные показатели вариации:

1. Размах вариации (R) представляет собой разность между
максимальным и минимальным значениями признака;

2. Среднее линейное отклонение (l)представляет собой среднюю арифметическую величину из абсолютных значений отклонений
отдельных признаков от их средней.

3. Дисперсия (средний квадрат отклонений) представляет собой среднюю арифметическую величину из квадратов отклонений значений признака от их средней.

4. Среднее квадратическое отклонение представляет собой
корень квадратный из дисперсии.

5. Коэффициент вариации представляет собой процентное
отношение среднего квадратического отклонения к средней
арифметической.

6. Коэффициент осцилляции представляет собой процентное
отношение размаха вариации к средней арифметической.

Условные обозначения в таблице 4.2:

х – конкретное значение признака;

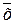- среднее значение признака;

n - число вариантов;

A – значение середины интервала с наибольшей частотой;

i –величина интервала.

Таблица 4.2